题目内容
 如图,矩形ABCD中,E,F分别是BC,CD上的点,且S△ABE=2,S△CEF=3,S△ADF=4,则S△AEF=________.
如图,矩形ABCD中,E,F分别是BC,CD上的点,且S△ABE=2,S△CEF=3,S△ADF=4,则S△AEF=________.
7
分析:设AB=x,CE=y,即可计算CF、DF、AD的值,且CD=CF+FD,根据AD、CD即可计算矩形ABCD的面积,根据S△AEF=S矩形ABCD-S△ABE-S△CEF-S△ADF即可计算△AEF的面积.
解答:设AB=x,CE=y.
∵∠B=∠C=90°,又S△ABE=2,
所以 •BE•x=2,即BE=
•BE•x=2,即BE=
同理CF=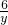 .
.
所以DF=CD-CF=AB-CF=x-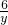 ,
,
AD= =
= .
.
而AD=BC,
即 =
= +y
+y
化简得(xy)2-10xy-24=0.
解得xy=12,
而矩形ABCD的面积=x( +y)=4+xy=16,
+y)=4+xy=16,
∴S△AEF=S矩形ABCD-S△ABE-S△CEF-S△ADF=7,
故答案为 7.
点评:本题考查了矩形面积的计算,考查了三角形面积的计算,考查了矩形各内角为直角的性质,本题中正确计算矩形ABCD的面积是解题的关键.
分析:设AB=x,CE=y,即可计算CF、DF、AD的值,且CD=CF+FD,根据AD、CD即可计算矩形ABCD的面积,根据S△AEF=S矩形ABCD-S△ABE-S△CEF-S△ADF即可计算△AEF的面积.
解答:设AB=x,CE=y.
∵∠B=∠C=90°,又S△ABE=2,
所以
 •BE•x=2,即BE=
•BE•x=2,即BE=
同理CF=
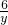 .
.所以DF=CD-CF=AB-CF=x-
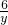 ,
,AD=
 =
= .
.而AD=BC,
即
 =
= +y
+y化简得(xy)2-10xy-24=0.
解得xy=12,
而矩形ABCD的面积=x(
 +y)=4+xy=16,
+y)=4+xy=16,∴S△AEF=S矩形ABCD-S△ABE-S△CEF-S△ADF=7,
故答案为 7.
点评:本题考查了矩形面积的计算,考查了三角形面积的计算,考查了矩形各内角为直角的性质,本题中正确计算矩形ABCD的面积是解题的关键.

练习册系列答案
相关题目
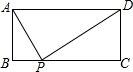 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )A、a≥
| ||
| B、a≥b | ||
C、a≥
| ||
| D、a≥2b |
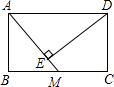 如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为
如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为 7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE=
7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE= (2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为
(2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为 (2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.
(2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.