题目内容
如图,在Rt△ABC中,∠ACB=90°,CP平分∠ACB,CP与AB交于点D,且 PA=PB.(1)请你过点P分别向AC、BC作垂线,垂足分别为点E、F,并判断四边形PECF的形状;
(2)求证:△PAB为等腰直角三角形;
(3)设PA=m,PC=n,试用m、n的代数式表示△ABC的周长;
(4)试探索当边AC、BC的长度变化时,
 的值是否发生变化,若不变,请直接写出这个不变的值,若变化,试说明理由.
的值是否发生变化,若不变,请直接写出这个不变的值,若变化,试说明理由.
【答案】分析:(1)四边形PECF的形状是正方形,易证四边形PECF是矩形,由角平分线的性质可知:PE=PF,所以四边形PECF是正方形;
(2)先根据角平分线及线段垂直平分线的作法作出P点,过点P分别作PE⊥AC、PF⊥CB,垂足为E、F,由全等三角形的判定定理得出Rt△APE≌Rt△BPF,再由全等三角形的性质即可判断出△PAB是等腰直角三角形;
(3)如图4,在Rt△PAB中,∠APB=90°,PA=PB,PA=m,所以AB= PA=
PA= ,由(2)中的证明过程可知,Rt△AEP≌Rt△BFP,可得AE=BF,CE=CF,所以CA+CB=CE+EA+CB=CE+CF=2CE,又PC=n,所以在正方形PECF中,CE=
,由(2)中的证明过程可知,Rt△AEP≌Rt△BFP,可得AE=BF,CE=CF,所以CA+CB=CE+EA+CB=CE+CF=2CE,又PC=n,所以在正方形PECF中,CE= PC=
PC= n.所以CA+CB=2CE=
n.所以CA+CB=2CE= .进而求出△ABC的周长;
.进而求出△ABC的周长;
(4)因为∠1=∠2=∠3=∠4=45°,且∠ADC=∠PDB,所以△ADC∽△PDB,故 ,即
,即 ,…①同理可得,△CDB∽△ADP,得到
,…①同理可得,△CDB∽△ADP,得到  ,…②又PA=PB,则①+②得:
,…②又PA=PB,则①+②得: =
= =
= =
= ,所以这个值仍不变为
,所以这个值仍不变为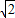 .
.
解答: 解:(1)四边形PECF的形状是正方形,理由如下:
解:(1)四边形PECF的形状是正方形,理由如下:
过点P分别作PE⊥AC、PF⊥CB,垂足分别为E、F(如图4)
∵∠ACB=90°,又由作图可知PE⊥AC、PF⊥CB,
∴四边形PECF是矩形,
又∵点P在∠ACB的角平分线上,
且PE⊥AC、PF⊥CB,
∴PE=PF,
∴四边形PECF是正方形;
(2)证明:在Rt△AEP和Rt△BFP中,
∵PE=PF,PA=PB,∠AEP=∠BFP=90°,
∴Rt△AEP≌Rt△BFP,
∴∠APE=∠BPF,
∵∠EPF=90°,从而∠APB=90°.
又因为PA=PB,
∴△PAB是等腰直角三角形;
(3)如图4,在Rt△PAB中,∠APB=90°,PA=PB,PA=m,
∴AB= PA=
PA= .
.
由(2)中的证明过程可知,Rt△AEP≌Rt△BFP,可得AE=BF,CE=CF,
∴CA+CB=CE+EA+CB=CE+CF=2CE,又PC=n,
∴在正方形PECF中,CE= PC=
PC= n.
n.
∴CA+CB=2CE= .
.
∴△ABC的周长为:AB+BC+CA= +
+ ;
;
(4)当边AC、BC的长度变化时, 的值不变,
的值不变, .理由如下:
.理由如下:
如图4,∵∠1=∠2=∠3=∠4=45°,且∠ADC=∠PDB,
∴△ADC∽△PDB,故 ,即
,即 ,…①
,…①
同理可得,△CDB∽△ADP,得到 ,…②
,…②
又PA=PB,则①+②得: =
= =
= =
= .
.
∴这个值仍不变为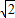 .
.
点评:本题考查的是相似形综合题,涉及到角平分线及线段垂直平分线的作法及性质、平行线的性质、全等三角形的判定与性质及三角形的面积公式,涉及面较广,难度较大.
(2)先根据角平分线及线段垂直平分线的作法作出P点,过点P分别作PE⊥AC、PF⊥CB,垂足为E、F,由全等三角形的判定定理得出Rt△APE≌Rt△BPF,再由全等三角形的性质即可判断出△PAB是等腰直角三角形;
(3)如图4,在Rt△PAB中,∠APB=90°,PA=PB,PA=m,所以AB=
 PA=
PA= ,由(2)中的证明过程可知,Rt△AEP≌Rt△BFP,可得AE=BF,CE=CF,所以CA+CB=CE+EA+CB=CE+CF=2CE,又PC=n,所以在正方形PECF中,CE=
,由(2)中的证明过程可知,Rt△AEP≌Rt△BFP,可得AE=BF,CE=CF,所以CA+CB=CE+EA+CB=CE+CF=2CE,又PC=n,所以在正方形PECF中,CE= PC=
PC= n.所以CA+CB=2CE=
n.所以CA+CB=2CE= .进而求出△ABC的周长;
.进而求出△ABC的周长;(4)因为∠1=∠2=∠3=∠4=45°,且∠ADC=∠PDB,所以△ADC∽△PDB,故
 ,即
,即 ,…①同理可得,△CDB∽△ADP,得到
,…①同理可得,△CDB∽△ADP,得到  ,…②又PA=PB,则①+②得:
,…②又PA=PB,则①+②得: =
= =
= =
= ,所以这个值仍不变为
,所以这个值仍不变为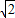 .
.解答:
 解:(1)四边形PECF的形状是正方形,理由如下:
解:(1)四边形PECF的形状是正方形,理由如下:过点P分别作PE⊥AC、PF⊥CB,垂足分别为E、F(如图4)
∵∠ACB=90°,又由作图可知PE⊥AC、PF⊥CB,
∴四边形PECF是矩形,
又∵点P在∠ACB的角平分线上,
且PE⊥AC、PF⊥CB,
∴PE=PF,
∴四边形PECF是正方形;
(2)证明:在Rt△AEP和Rt△BFP中,
∵PE=PF,PA=PB,∠AEP=∠BFP=90°,
∴Rt△AEP≌Rt△BFP,
∴∠APE=∠BPF,
∵∠EPF=90°,从而∠APB=90°.
又因为PA=PB,
∴△PAB是等腰直角三角形;
(3)如图4,在Rt△PAB中,∠APB=90°,PA=PB,PA=m,
∴AB=
 PA=
PA= .
. 由(2)中的证明过程可知,Rt△AEP≌Rt△BFP,可得AE=BF,CE=CF,
∴CA+CB=CE+EA+CB=CE+CF=2CE,又PC=n,
∴在正方形PECF中,CE=
 PC=
PC= n.
n.∴CA+CB=2CE=
 .
.∴△ABC的周长为:AB+BC+CA=
 +
+ ;
;(4)当边AC、BC的长度变化时,
 的值不变,
的值不变, .理由如下:
.理由如下:如图4,∵∠1=∠2=∠3=∠4=45°,且∠ADC=∠PDB,
∴△ADC∽△PDB,故
 ,即
,即 ,…①
,…①同理可得,△CDB∽△ADP,得到
 ,…②
,…②又PA=PB,则①+②得:
 =
= =
= =
= .
.∴这个值仍不变为
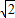 .
.点评:本题考查的是相似形综合题,涉及到角平分线及线段垂直平分线的作法及性质、平行线的性质、全等三角形的判定与性质及三角形的面积公式,涉及面较广,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F. 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离.
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离. 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直. 如图,在Rt△ABC中,BD⊥AC,sinA=
如图,在Rt△ABC中,BD⊥AC,sinA= 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).