题目内容
 如图,外切于P点的⊙O1和⊙O2的半径分别为2cm和4cm,连心线交⊙O1于点A,交⊙O2于点B,AC与⊙O2相切于点C,连接PC,则PC的长为( )
如图,外切于P点的⊙O1和⊙O2的半径分别为2cm和4cm,连心线交⊙O1于点A,交⊙O2于点B,AC与⊙O2相切于点C,连接PC,则PC的长为( )分析:在直角△ACO2中利用三角函数即可求得∠CO2P的度数,即可证得△O2CP是等边三角形,则可以求解.
解答:解:在直角△ACO2中,AO2=4+4=8,O2C=4,
则sinA=
=
,
∴∠A=30°,
∴∠CO2P=60°
又∵O2C=O2P,
∴△O2CP是等边三角形,
∴PC=O2C=4cm.
故选C.
则sinA=
| 4 |
| 8 |
| 1 |
| 2 |
∴∠A=30°,
∴∠CO2P=60°
又∵O2C=O2P,
∴△O2CP是等边三角形,
∴PC=O2C=4cm.
故选C.
点评:本题考查了相切两圆的性质以及三角函数,正确证明△O2CP是等边三角形是关键.

练习册系列答案
相关题目
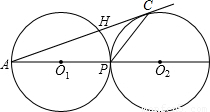
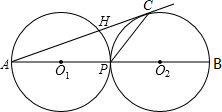 如图,外切于P点的⊙O1和⊙O2是半径为3cm的等圆,连心线交⊙O1于点A,交⊙O2于点B,AC与⊙O2相切于点C,连接PC,则PC的长为( )
如图,外切于P点的⊙O1和⊙O2是半径为3cm的等圆,连心线交⊙O1于点A,交⊙O2于点B,AC与⊙O2相切于点C,连接PC,则PC的长为( )A、2
| ||
B、3
| ||
| C、3cm | ||
| D、4.5cm |
 cm
cm cm
cm
 cm
cm cm
cm
 cm
cm cm
cm