题目内容
(2012•顺平县模拟)已知:如图1,在△ABC中,AB=AC=5,AD为底边BC上的高,且AD=3.将△ACD沿箭头所示的方向平移,得到△A'CD'(如图2),A'D'交AB于E,A'C分别交AB、AD 于G、F,以D'D为直径作⊙O,设BD'的长为x,⊙O的面积为 y.
(1)求y与x的函数关系式及自变量x的取值范围(不考虑端点);
(2)当BD'的长为多少时,⊙O的面积与△ABD的面积相等?(π取3,结果精确到 0.1)
(3)连接EF,求EF与⊙O 相切时x的值.

(1)求y与x的函数关系式及自变量x的取值范围(不考虑端点);
(2)当BD'的长为多少时,⊙O的面积与△ABD的面积相等?(π取3,结果精确到 0.1)
(3)连接EF,求EF与⊙O 相切时x的值.

分析:(1)首先表示出圆的半径,才能表示出面积,(2)求出△ABD的面积,在表示出⊙O的面积,即可求出.
(3)证明四边形ED′DF是矩形,再利用三角形相似求出.
(3)证明四边形ED′DF是矩形,再利用三角形相似求出.
解答: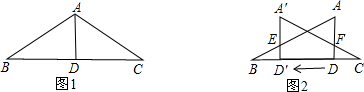 解:(1)∵AB=AC=5,AD为底边BC上的高,且AD=3.
解:(1)∵AB=AC=5,AD为底边BC上的高,且AD=3.
∴BD=4,设BD'的长为x,⊙O的面积为y,
∴y=π(
) 2=π(2-x)2(0≤x≤4);
(2)∵S△ABD=
×3×4=6,y=π(2-x)2=3(2-x)2,
∴(2-x)2=2,
∴解得:x=2±
,
BD′=2±
时,⊙O的面积与△ABD的面积相等;
(3)连接EF,
∵△BD′E≌△CDF,
∴ED′=FD,ED′∥FD,∠FDC=90°,
∴四边形ED′DF是矩形,
∴DD′=EF,ED′=
DD′,
∵△BED′∽△BAD,
∴
=
,
∴
=
,
解得:x=
,
EF与⊙O 相切时x的值为
.
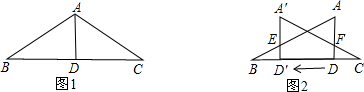 解:(1)∵AB=AC=5,AD为底边BC上的高,且AD=3.
解:(1)∵AB=AC=5,AD为底边BC上的高,且AD=3.∴BD=4,设BD'的长为x,⊙O的面积为y,
∴y=π(
| 4-2x |
| 2 |
(2)∵S△ABD=
| 1 |
| 2 |
∴(2-x)2=2,
∴解得:x=2±
| 2 |
BD′=2±
| 2 |
(3)连接EF,
∵△BD′E≌△CDF,
∴ED′=FD,ED′∥FD,∠FDC=90°,
∴四边形ED′DF是矩形,
∴DD′=EF,ED′=
| 1 |
| 2 |
∵△BED′∽△BAD,
∴
| BD′ |
| BD |
| ED′ |
| AD |
∴
| x |
| 4 |
| ||
| 3 |
解得:x=
| 8 |
| 5 |
EF与⊙O 相切时x的值为
| 8 |
| 5 |
点评:此题主要考查了相似三角形的判定与性质,以及矩形的判定和求函数关系式,题目难度不大,非常典型.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 (2012•顺平县模拟)如图,正方形ABCD的边长为4,E是BC边的中点,P是对角线BD上一个动点,则PE+PC的最小值是( )
(2012•顺平县模拟)如图,正方形ABCD的边长为4,E是BC边的中点,P是对角线BD上一个动点,则PE+PC的最小值是( )