题目内容
如图，一根木棒（AB）长2a，斜靠在与地面（OM）垂直的墙（ON）上，与地面的倾斜角（∠ABO）为60°，若木棒A端沿直线ON下滑，且B端沿直线OM向右滑行（NO⊥OM），于是木棒的中点P也随之运动，已知A端下滑到A'时，求中点P随之运动到P'时经过的路线长．
∵AP=OP，∠ABO=60°
∴∠AOP=30°，∠POB=60°．
∵OP′=P′B′，
∵△A′OB′是等腰直角三角形，
∴∠A′B′O=45°
∴∠B′OP′=45°
∴∠POP'=15°
∵AB=2a．点P为AB的中点
∴OP=a
∴弧PP'=
=
a．
∴∠AOP=30°，∠POB=60°．
∵OP′=P′B′，
∵△A′OB′是等腰直角三角形，
∴∠A′B′O=45°
∴∠B′OP′=45°
∴∠POP'=15°
∵AB=2a．点P为AB的中点
∴OP=a
∴弧PP'=
| 15πa |
| 180 |
| π |
| 12 |
练习册系列答案
相关题目
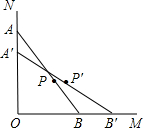（2011•自贡）如图，一根木棒（AB）长为2a，斜靠在与地面（OM）垂直的墙壁（ON）上，与地面的倾斜角（∠ABO）为60°，当木棒A端沿N0向下滑动到A′，AA′=
如图，一根木棒（AB）长2a，斜靠在与地面（OM）垂直的墙（ON）上，与地面的倾斜角（∠ABO）为60°，若木棒A端沿直线ON下滑，且B端沿直线OM向右滑行（NO⊥OM），于是木棒的中点P也随之运动，已知A端下滑到A'时，求中点P随之运动到P'时经过的路线长．
，B端沿直线OM向右滑动到B′，则木棒中点从P随之运动到P′所经过的路径长为 ．
