��Ŀ����
����Ŀ���׳���![]() �س�������ʻ��
�س�������ʻ��![]() �أ�����
�أ�����![]() �غ�������ԭ·ԭ�ٷ���
�غ�������ԭ·ԭ�ٷ���![]() �أ��ҳ���
�أ��ҳ���![]() �س�������ͬ·������ʻ��
�س�������ͬ·������ʻ��![]() �أ�����
�أ�����![]() Сʱ���ҳ��������;��ͣ��
Сʱ���ҳ��������;��ͣ��![]() Сʱ��Ȼ�������ԭ��ʻ��
Сʱ��Ȼ�������ԭ��ʻ��![]() �أ��ҳ�����ʻ�����е��ٶ���
�أ��ҳ�����ʻ�����е��ٶ���![]() ǧ��/ʱ���׳����ҳ���
ǧ��/ʱ���׳����ҳ���![]() Сʱ����
Сʱ����![]() �أ���������Գ����ص�·��
�أ���������Գ����ص�·��![]() ǧ����׳���ʻʱ��
ǧ����׳���ʻʱ��![]() Сʱ֮��ĺ�����ϵ��ͼ��ʾ������ͼ����Ϣ����������⣺
Сʱ֮��ĺ�����ϵ��ͼ��ʾ������ͼ����Ϣ����������⣺
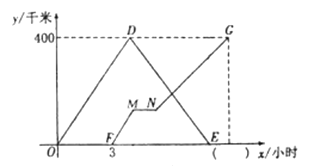
��1��д���׳���ʻ���ٶȣ���ֱ��д��ͼ����������ȷ����__ __
��2����׳���![]() �ط���
�ط���![]() �صĹ����У�
�صĹ����У�![]() ��
��![]() �ĺ�����ϵʽ(����Ҫд���Ա���
�ĺ�����ϵʽ(����Ҫд���Ա���![]() ��ȡֵ��Χ)��
��ȡֵ��Χ)��
��3��ֱ��д���׳���������Сʱ������ǡ�����![]() ǧ�ף�
ǧ�ף�
���𰸡���1��9����2��![]() ����3��
����3��![]() ��1��5Сʱ
��1��5Сʱ
��������
��1����������ͺ���ͼ���е����ݿ�����ü׳���ʻ�ٶȺ�ͼ��������Ӧ��������ݣ�
��2�����ݺ���ͼ���е����ݿ��Եõ��׳���B�ط���A�صĹ����У�y��x�ĺ�����ϵʽ��
��3��������������г���Ӧ�ķ��̣�������Խ����
��1���ҳ���B�ص�A���õ�ʱ��Ϊ��400��80��5��Сʱ����
�׳����ٶ�Ϊ��400��[��3��5��11����2]��100��ǧ��/Сʱ����
ͼ����������ȷ������3��5��1��9��
�ʴ�Ϊ��9��
��2����׳���B�ط���A�صĹ����У�y��x�ĺ�����ϵʽΪy��kx��b��
�ߵ�D��4��400������E��8��0�����߶�DE�ϣ�
��![]() ����
����![]() ��
��
���׳���B�ط���A�صĹ����У�y��x�ĺ�����ϵʽ��y��100x��800��
��3���ټ���B��ǰ�����ҳ�����tСʱ������ǡ�����80ǧ�ף�
80t��100��t��3����40080��
��ã�t��![]() ��
��
�ڵ��ҳ���1Сʱʱ�����ߵ�·����1��80��80��ǧ�ף�����ʱ�պõ��ҵأ����ҵľ����ǣ�80ǧ�ף�
�ҳ���1Сʱ�����ҳ�����tСʱ������ǡ�����80ǧ�ף�
�۵��ҳ���2Сʱʱ�����ߵ�·����1��80��80��ǧ�ף����״�B���ߵ�·���ǣ�100����3��21����100��ǧ�ף�����ʱ���ҵľ����ǣ�10080��20��ǧ�ף���
���׳���B�ط���A�صĹ����У���tСʱ���������80ǧ�ף�
100��t1��80��t1����80��80��t1����80��400��
��ã�t��5��t��5��
���ҳ�����![]() Сʱ��1Сʱ��5Сʱʱ������ǡ�����80ǧ�ף�
Сʱ��1Сʱ��5Сʱʱ������ǡ�����80ǧ�ף�

 ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�