题目内容
已知:正方形ABCD,点A、B在x轴上,直线y=mx+n( <n<m)过点A、C
<n<m)过点A、C 交y轴于点E,S△AOE=2S正方形ABCD,抛物线y=ax2+bx+c过点A、B,且顶点G在直线y=mx+n上,抛物线y与轴交于点F.
交y轴于点E,S△AOE=2S正方形ABCD,抛物线y=ax2+bx+c过点A、B,且顶点G在直线y=mx+n上,抛物线y与轴交于点F.
(1)求a•b•c的值;
(2)求S△AGF的范围.
解:(1)直线AE中,y=mx+n,则E(0,n);
∵正方形ABCD,
∴AB=BC,则tan∠CAB=1,
∴OA=OE=n,即A(-n,0);
△AOE中,AO=n,OE=n,
则S△AOE= OA•OE=
OA•OE= ,又S正方形ABCD=AB2,
,又S正方形ABCD=AB2,
∵S△AOE=2S正方形ABCD,
∴ n2=2AB2,即AB=
n2=2AB2,即AB= n,
n,
故OB=OA-AB=n- n=
n= n,即B(-
n,即B(- n,0);
n,0);
∴A(-n,0),B(- n,0).
n,0).
∵G是抛物线的顶点,且A(-n,0),B(- n,0),
n,0),
∴G点的横坐标为- n;
n;
易知G是线段AC的中点,故BC=AB=2yG,
∴G点的纵坐标为 n;
n;
即G(- n,
n, n);
n);
设抛物线的解析式为y=a(x+ n)2+
n)2+ n,将A(-n,0)代入上式,得:
n,将A(-n,0)代入上式,得:
a× n2+
n2+ n=0,即a=-
n=0,即a=- ;
;
∴y=- (x+
(x+ n)2+
n)2+ n=-
n=- x2-6x-2n;
x2-6x-2n;
故abc=(- )×(-6)×(-2n)=-48.
)×(-6)×(-2n)=-48.
(2)根据(1)得到的抛物线解析式,易知F(0,-2n);
∵E(0,n),A(-n,0),G(- n,
n, n),
n),
∴S△AEF= EF•OA=
EF•OA=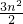 ,S△EGF=
,S△EGF= EF•|xG|=
EF•|xG|= n2,
n2,
∴S△AGF=S△AEF-S△EGF= n2-
n2- n2=
n2= n2,又n>
n2,又n> ,
,
故S△AGF的范围为:S△AGF>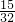 .
.
分析:(1)根据直线AE的解析式可得到点E的坐标,根据正方形ABCD的边长相等得到AB=BC,即AO=OE,由此可求得点A的坐标;易求得△AOE的面积,即可得到正方形ABCD的面积,由于AB=BC,可用AB表示出正方形ABCD的面积,进而可得到AB的值(含n的表达式),由此可确定点B的坐标.由于点G是抛物线的顶点,即在抛物线的对称轴上,根据A、B的坐标,可求得点G的横坐标,而G点在直线AE上,那么G点的纵坐标应该是AB的 (由于AB=BC=2yG),由此可确定点G的坐标;可将抛物线设为顶点坐标式,将A或B的坐标代入其中,即可求出含n的抛物线解析式,进而可求出abc的值;
(由于AB=BC=2yG),由此可确定点G的坐标;可将抛物线设为顶点坐标式,将A或B的坐标代入其中,即可求出含n的抛物线解析式,进而可求出abc的值;
(2)△AGF的面积无法直接求出,分析图形后可知△AGF的面积为△AEF、△EGF的面积差,这两个三角形的顶点的坐标都已求出,即可得到△AGF的面积表达式(含n的式子),根据已知的n的取值范围,即可求得△AGF的面积范围.
点评:此题是二次函数的综合题,涉及到函数图象与坐标轴交点坐标的求法、函数解析式的确定、图形面积的求法等重要知识,由于本题中大部分数据都是字母,乍看之下无从下手,但是只要将字母当做已知数来对待,即可按照常规思路解决问题.
∵正方形ABCD,
∴AB=BC,则tan∠CAB=1,
∴OA=OE=n,即A(-n,0);
△AOE中,AO=n,OE=n,
则S△AOE=
 OA•OE=
OA•OE= ,又S正方形ABCD=AB2,
,又S正方形ABCD=AB2,∵S△AOE=2S正方形ABCD,
∴
 n2=2AB2,即AB=
n2=2AB2,即AB= n,
n,故OB=OA-AB=n-
 n=
n= n,即B(-
n,即B(- n,0);
n,0);∴A(-n,0),B(-
 n,0).
n,0).∵G是抛物线的顶点,且A(-n,0),B(-
 n,0),
n,0),∴G点的横坐标为-
 n;
n;易知G是线段AC的中点,故BC=AB=2yG,
∴G点的纵坐标为
 n;
n;即G(-
 n,
n, n);
n);设抛物线的解析式为y=a(x+
 n)2+
n)2+ n,将A(-n,0)代入上式,得:
n,将A(-n,0)代入上式,得:a×
 n2+
n2+ n=0,即a=-
n=0,即a=- ;
;∴y=-
 (x+
(x+ n)2+
n)2+ n=-
n=- x2-6x-2n;
x2-6x-2n;故abc=(-
 )×(-6)×(-2n)=-48.
)×(-6)×(-2n)=-48.(2)根据(1)得到的抛物线解析式,易知F(0,-2n);
∵E(0,n),A(-n,0),G(-
 n,
n, n),
n),∴S△AEF=
 EF•OA=
EF•OA=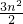 ,S△EGF=
,S△EGF= EF•|xG|=
EF•|xG|= n2,
n2,∴S△AGF=S△AEF-S△EGF=
 n2-
n2- n2=
n2= n2,又n>
n2,又n> ,
,故S△AGF的范围为:S△AGF>
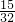 .
.分析:(1)根据直线AE的解析式可得到点E的坐标,根据正方形ABCD的边长相等得到AB=BC,即AO=OE,由此可求得点A的坐标;易求得△AOE的面积,即可得到正方形ABCD的面积,由于AB=BC,可用AB表示出正方形ABCD的面积,进而可得到AB的值(含n的表达式),由此可确定点B的坐标.由于点G是抛物线的顶点,即在抛物线的对称轴上,根据A、B的坐标,可求得点G的横坐标,而G点在直线AE上,那么G点的纵坐标应该是AB的
 (由于AB=BC=2yG),由此可确定点G的坐标;可将抛物线设为顶点坐标式,将A或B的坐标代入其中,即可求出含n的抛物线解析式,进而可求出abc的值;
(由于AB=BC=2yG),由此可确定点G的坐标;可将抛物线设为顶点坐标式,将A或B的坐标代入其中,即可求出含n的抛物线解析式,进而可求出abc的值;(2)△AGF的面积无法直接求出,分析图形后可知△AGF的面积为△AEF、△EGF的面积差,这两个三角形的顶点的坐标都已求出,即可得到△AGF的面积表达式(含n的式子),根据已知的n的取值范围,即可求得△AGF的面积范围.
点评:此题是二次函数的综合题,涉及到函数图象与坐标轴交点坐标的求法、函数解析式的确定、图形面积的求法等重要知识,由于本题中大部分数据都是字母,乍看之下无从下手,但是只要将字母当做已知数来对待,即可按照常规思路解决问题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )
如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )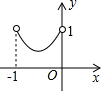
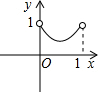
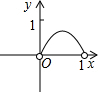
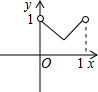
 由.
由. s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒.
s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒. 18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点.
18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点. 如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=