题目内容
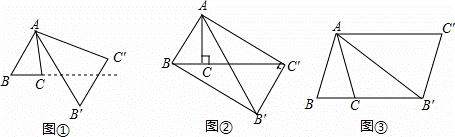
将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′，即如图①，我们将这种变换记为[θ，n]．
（1）如图①，对△ABC作变换[60°，
]得△AB′C′，则S△AB′C′：S△ABC= 3 ；直线BC与直线B′C′所夹的锐角为 60 度；
（2）如图②，△ABC中，∠BAC=30°，∠ACB=90°，对△ABC 作变换[θ，n]得△AB'C'，使点B、C、C′在同一直线上，且四边形ABB'C'为矩形，求θ和n的值；
（4）如图③，△ABC中，AB=AC，∠BAC=36°，BC=l，对△ABC作变换[θ，n]得△AB′C′，使点B、C、B′在同一直线上，且四边形ABB'C'为平行四边形，求θ和n的值．
|
考点： | 相似三角形的判定与性质；解一元二次方程-公式法；平行四边形的性质；矩形的性质；旋转的性质。 |
| 专题： | 代数几何综合题。 |
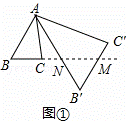
| 分析： | （1）由旋转与相似的性质，即可得S△AB′C′：S△ABC=3，然后由△ABN与△B′MN中，∠B=∠B （2）由四边形 ABB′C′是矩形，可得∠BAC′=90°，然后由θ=∠CAC′=∠BAC′﹣∠BAC，即可求得θ的度数，又由含30°角的直角三角形的性质，即可求得n的值； （3）由四边形ABB′C′是平行四边形，易求得θ=∠CAC′=∠ACB=72°，又由△ABC∽△B′BA，根据相似三角形的对应边成比例，易得AB2=CB•BB′=CB（BC+CB′），继而求得答案． |
| 解答： | 解：（1）根据题意得：△ABC∽△AB′C′， ∴S△AB′C′：S△ABC=（ ∵∠ANB=∠B′NM， ∴∠BMB′=∠BAB′=60°； 故答案为：3，60； （2）∵四边形 ABB′C′是矩形， ∴∠BAC′=90°． ∴θ=∠CAC′=∠BAC′﹣∠BAC=90°﹣30°=60°． 在 Rt△ABC 中，∠ABB'=90°，∠BAB′=60°， ∴∠AB′B=30°， ∴n= （3）∵四边形ABB′C′是平行四边形，[来源:学科网ZXXK] ∴AC′∥BB′， 又∵∠BAC=36°， ∴θ=∠CAC′=∠ACB=72°． ∴∠C′AB′=∠BAC=36°，而∠B=∠B， ∴△ABC∽△B′BA， ∴AB：BB′=CB：AB， ∴AB2=CB•BB′=CB（BC+CB′）， 而 CB′=AC=AB=B′C′，BC=1， ∴AB2=1（1+AB）， ∴AB= ∵AB＞0， ∴n=
|
| 点评： | 此题考查了相似三角形的判定与性质、直角三角形的性质、旋转的性质、矩形的性质以及平行四边形的性质．此题综合性较强，难度较大，注意数形结合思想与方程思想的应用，注意辅助线的作法． |
′，∠ANB=∠B′NM，可得∠BMB′=∠BAB′，即可求得直线BC与直线B′C′所夹的锐角的度数；
）2=（
）2=3，∠B=∠B
′，
=2；
，
=
．
21、在平面直角坐标系中有△ABC与△A1B1C1，其位置如图所示，
如图，△ABC中，∠CAB=70°，将△ABC绕点A按逆时钟方向旋转，设旋转角为α（0°＜α＜180°），得到△AB′C′，若CC′∥AB，则旋转角α的度数为（ ）
轴对称的△A1B1C1；
所得的△A2B2C2；
轴对称的△A1B1C1；
所得的△A2B2C2；
如图，△ABC中，∠CAB=70°，将△ABC绕点A按逆时钟方向旋转，设旋转角为α（0°＜α＜180°），得到△AB′C′，若CC′∥AB，则旋转角α的度数为