题目内容
如图，A、B是半径为3的⊙O上的两点，若∠AOB=120°，C是 | AB |
分析：通过等弧所对的圆心角相等和∠AOB=120°，得到△AOC和△BOC都是等边三角形，再求出四边形AOBC的周长．
解答：解：∵C是
的中点
∴∠AOC=∠BOC，而∠AOB=120°
∴∠AOC=∠BOC=60°
∴△AOC和△BOC都是等边三角形
∴OA=OB=CA=CB=3
所以四边形AOBC的周长等于12．
故填12．
|
| AB |
∴∠AOC=∠BOC，而∠AOB=120°
∴∠AOC=∠BOC=60°
∴△AOC和△BOC都是等边三角形
∴OA=OB=CA=CB=3
所以四边形AOBC的周长等于12．
故填12．
点评：掌握等弧所对的圆心角相等；熟练掌握等边三角形的判定和性质定理．
练习册系列答案
相关题目
如图，若四边形ABCD是半径为1的⊙O的内接正方形，则图中四个弓形（即四个阴影部分）的面积和为（ ）| A、（2π-2）cm2 | B、（2π-1）cm2 | C、（π-2）cm2 | D、（π-1）cm2 |
Q分别为PB、弧CQB上的切点．
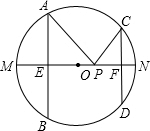如图，AB、CD是半径为5的⊙O的两条弦，AB=8，CD=6，MN是直径，AB⊥MN于点E，CD⊥MN于点F，P为EF上的任意一点，则PA+PC的最小值为多少？
如图，实线部分是半径为9m的两条等弧组成的花圃，若每条弧所在的圆都经过另一个圆的圆心，则花圃的周长为（ ）