Question

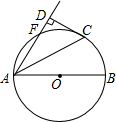如图，AB是⊙O的直径，点F，C是⊙O上两点，且

AF

=

FC

=

CB

，连接AC，AF，过点C作CD⊥AF交AF延长线于点D，垂足为D．
（1）求证：CD是⊙O的切线；
（2）若CD=2

3

，求⊙O的半径．

Answer 1

考点：切线的判定,三角形三边关系,圆周角定理

专题：几何图形问题

分析：（1）连结OC，由

FC

=

BC

，根据圆周角定理得∠FAC=∠BAC，而∠OAC=∠OCA，则∠FAC=∠OCA，可判断OC∥AF，由于CD⊥AF，所以OC⊥CD，然后根据切线的判定定理得到CD是⊙O的切线；
（2）连结BC，由AB为直径得∠ACB=90°，由

AF

=

FC

=

CB

得∠BOC=60°，则∠BAC=30°，所以∠DAC=30°，在Rt△ADC中，利用含30度的直角三角形三边的关系得AC=2CD=4

3

，在Rt△ACB中，利用含30度的直角三角形三边的关系得BC=

3

3

AC=4，AB=2BC=8，所以⊙O的半径为4．

解答：（1）证明：连结OC，如图，
∵

FC

=

BC

，
∴∠FAC=∠BAC，
∵OA=OC，
∴∠OAC=∠OCA，
∴∠FAC=∠OCA，
∴OC∥AF，
∵CD⊥AF，
∴OC⊥CD，
∴CD是⊙O的切线；

（2）解：连结BC，如图，
∵AB为直径，
∴∠ACB=90°，
∵

AF

=

FC

=

CB

，
∴∠BOC=

1

3

×180°=60°，
∴∠BAC=30°，
∴∠DAC=30°，
在Rt△ADC中，CD=2

3

，
∴AC=2CD=4

3

，
在Rt△ACB中，BC=

3

3

AC=

3

3

×4

3

=4，
∴AB=2BC=8，
∴⊙O的半径为4．

点评：本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了圆周角定理和含30度的直角三角形三边的关系．