Question

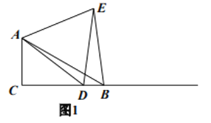
【题目】如图，已知ABCD，点E是BC边上的一点，将边AD延长至点F，使∠AFC＝∠DEC.

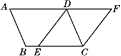
(1)求证：四边形DECF是平行四边形；

(2)若AB＝13，DF＝14，tan A＝，求CF的长．

Answer 1

【答案】（1）见解析；（2）15

【解析】 试题分析：（1）由已知可知AD∥BC，从而得∠ADE＝∠DEC，再根据∠AFC＝∠DEC，从而得∠AFC＝∠ADE，继而得DE∥FC，问题得证；

（2）过点D作DH⊥BC于点H，由已知得到∠BCD＝∠A，AB＝CD＝13，再根据tan A＝tan∠DCH＝，从而得到DH、CH的长，从而得到CE、DE的长，继而得CF的长.

试题解析：（1）∵四边形ABCD是平行四边形，

∴AD∥BC，∴∠ADE＝∠DEC，

又∵∠AFC＝∠DEC，∴∠AFC＝∠ADE，

∴DE∥FC，

∴四边形DECF是平行四边形；

（2）过点D作DH⊥BC于点H，如图所示．

∵四边形ABCD是平行四边形，

∴∠BCD＝∠A，AB＝CD＝13，

又∵tan A＝＝tan∠DCH＝，

∴DH＝12，CH＝5，

∵DF＝14，∴CE＝14，

∴EH＝9，

∴DE＝＝15，

∴CF＝DE＝15.