题目内容
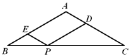
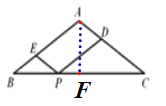
【题目】在等腰三角形ABC中，AB=AC，∠B=30°，BC=
cm，P是BC上任意一点，过P作PD//AB，PE//AC，则PE+PD的值为__________________.
【答案】6
【解析】先证明BE=PE，AE=PD，把求PE+PD的长转化为求AB的长，然后作AF⊥BC于点F，在Rt△ABF中求AB的长即可.
∵AB=AC，∠B=30°，
∴∠B=∠C=30°，
∵PE//AC，
∴∠BPE=∠C=30°，
∴∠BPE=∠B=30°，
∴BE=PE.
∵PD//AB，PE//AC，
∴四边形AEPD是平行四边形，
∴AE=PD，
∴PE+PD=BE+AE=AB.
作AF⊥BC于点F.
∴
,
.
∵AB2=AF2+BF2,
∴
,
∴AB=6,
故答案为：6.
练习册系列答案
相关题目
