题目内容
如图所示，△ABC中，∠ACB=90°，CD⊥AB于点D，若BD：AD=1：4，则tan∠BCD的值是（▲）
A． | B． | C． | D．2 |
C 解：∵∠ACB=90°，CD⊥AB于D，
∴∠BCD=∠CAD=90°-∠ACD，∠BDC=∠CDA=90°，
∴△BCD∽△CAD． （2分）
∴
，
即CD
=BD×AD． （3分）
∵BD：AD=1：4，
∴设BD为x，则AD为4x．
∴CD=2X． （4分）
在△BCD中，∠BDC=90°，∴tan∠BCD=
． 故选C
∴∠BCD=∠CAD=90°-∠ACD，∠BDC=∠CDA=90°，
∴△BCD∽△CAD． （2分）
∴
，即CD
=BD×AD． （3分）∵BD：AD=1：4，
∴设BD为x，则AD为4x．
∴CD=2X． （4分）
在△BCD中，∠BDC=90°，∴tan∠BCD=
． 故选C 
练习册系列答案
全能测控期末小状元系列答案
相关题目
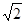≈1.414，
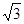≈1.732）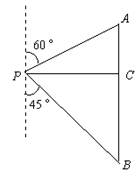
，
，
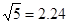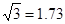，结果保留两个有效数字).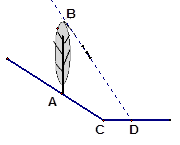
中，
，则
=___________．
中，AB=BD=2，则sin∠CAB的值为 ．
