题目内容
如图,将矩形 沿
沿 折叠,使
折叠,使 点落在
点落在 边上的
边上的 点处;再将矩形
点处;再将矩形 沿
沿 折叠,使
折叠,使 点落在
点落在 点处且
点处且 过
过 点.
点.

(1)求证:四边形 是平行四边形;
是平行四边形;
(2)当 是多少度时,四边形
是多少度时,四边形 为菱形?试说明理由.
为菱形?试说明理由.
【答案】
(1)证明见解析;(2)当∠B1FE=60°时,四边形EFGB为菱形,理由见解析.
【解析】
试题分析:(1)由题意,∠B1FE=∠FEB,结合∠B1FE=∠BFE,得BE=BF,同理可得FG=BF,即BE=FG,结合BE∥FG,得到四边形BEFG是平行四边形;
(2)当∠B1FE=60°时,四边形EFGB为菱形,由∠B1FE=60°,得∠BFE=∠BEF=60°,得到△BEF为等边三角形,即BE=EF,结合四边形BEFG是平行四边形,即可证得.
试题解析:(1)∵A1D1∥B1C1,
∴∠B1FE=∠FEB.
又∵∠B1FE=∠BFE,
∴∠FEB=∠BFE.
∴BE=BF.
同理可得:FG=BF.
∴BE=FG,
又∵BE∥FG,
∴四边形BEFG是平行四边形;
(2)当∠B1FE=60°时,四边形EFGB为菱形.
理由如下:
∵∠B1FE=60°,
∴∠BFE=∠BEF=60°,
∴△BEF为等边三角形,即BE=EF.
∵四边形BEFG是平行四边形,BE=EF.
∴四边形BEFG是菱形(一组邻边相等的平行四边形是菱形).
考点:1.翻折变换(折叠问题),2.平行四边形的判定,3.菱形的判定,4.矩形的性质.

练习册系列答案
相关题目
 4、如图,将矩形沿对称轴折叠,在对称轴处剪下一块,余下部分的展开图为( )
4、如图,将矩形沿对称轴折叠,在对称轴处剪下一块,余下部分的展开图为( )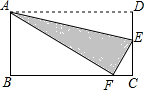 如图,将矩形沿AE折叠,使D落在BC上的点F处,AB=8,BC=10,则EC的长是( )
如图,将矩形沿AE折叠,使D落在BC上的点F处,AB=8,BC=10,则EC的长是( ) 沿直线
沿直线 折叠,顶点
折叠,顶点 恰好落在
恰好落在 边上
边上 点处,已知
点处,已知 ,
, ,则图中阴影部分面积为
__.
,则图中阴影部分面积为
__. 









