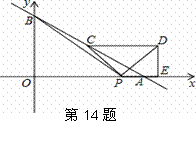
题目内容
如图,抛物线 (
( )与
)与 轴的一个交点为
轴的一个交点为 (
( ,0),点
,0),点 ,
, 的坐标分别为
的坐标分别为 (1,0),
(1,0), (4,0),分别过点
(4,0),分别过点 ,
, 作
作 轴的平行线,交抛物线于点
轴的平行线,交抛物线于点 ,
, ,连结
,连结 ,
, 和
和 ,设
,设 的面积为
的面积为 .
.
(1)证明:对于任何 (
( ),都有
),都有 ;
;
(2)当 时,求
时,求 与
与 的函数关系式;
的函数关系式;
(3)当 且
且 时,求
时,求 的值.
的值.
 |
(1)证明:∵点 在抛物线上,
在抛物线上,
∴点 的横坐标为1,纵坐标为
的横坐标为1,纵坐标为 (
( ), 1分
), 1分
 ∴
∴ ,又
,又 ,∴
,∴ , 2分
, 2分
∵ ,∴
,∴ ; 3分
; 3分
(2)当 时,
时,
 , 4分
, 4分
 ,
,
∴ (
( ); 6分
); 6分
(3)令 ,解得
,解得 ,
, , 8分
, 8分
∵ ,∴
,∴ 舍去,∴
舍去,∴ . 9分
. 9分

练习册系列答案
相关题目
中国男子国家足球队冲击 2010 年南非世界杯失利后,某新闻机构就中国足球环境问题随机调查
了 400 人,其结果如下:
| 意见 | 非常不满意 | 不满意 | 有一点满意 | 满意 |
| 人数 | 200 | 160 | 32 | 8 |
| 百分比 |
(1)计算出每一种意见人数占总调查人数的百分比(填在以上空格中); 请画出反映此调查结果的扇形统计图;(3)从统计图中你能得出什么结论?说说你的理由.
 经过抛物线y=ax2+bx的顶点(-
经过抛物线y=ax2+bx的顶点(-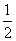 ,m)(m>0),则有……( )
,m)(m>0),则有……( ) .a<k<0
.a<k<0
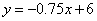 与x,y轴分别交于A,B,C
与x,y轴分别交于A,B,C ),当以P,D,E为
),当以P,D,E为