题目内容
【题目】如图，长方形
中，
，
.点
从点
出发，沿
匀速运动；点
从点
出发，沿
的路径匀速运动.两点同时出发，在
点处首次相遇后，点的运动速度每秒提高了
，并沿
的路径匀速运动；点保持速度不变，继续沿原路径匀速运动，某一时刻两点在长方形某一边上的
点处第二次相遇.若点的速度为
.
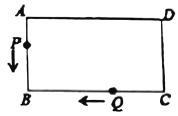
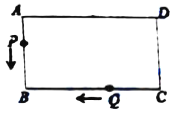
备用图
（1）点原来的速度为___________
.
（2），两点在点处首次相遇后，再经过___________秒后第二次在点相遇.
（3）点在___________边上.此时
___________
.
（4）在点相遇后，两点沿原来的方向继续前进.又经历了
次相遇后停止运动，请问此时两点停在长方形边上的什么位置？
【答案】（1）
；（2）
；AD; 
；（4）Q点移动99次后与P点相遇在AD上，且距离A点
处.
【解析】
（1）根据题意可得点
原来的速度为
点的速度的两倍，故可求解；
（2）设经过xs相遇，根据题意列出方程即可求解；
（3）由（2）可得到移动的路程，即可求出E点位置，再求出
；
（4）根据每次相遇移动的时间相等，故求出Q点移动99次后的路程，即可得到终点位置.
（1）∵两点同时出发，在
点处首次相遇后，
， 点的速度为
.
∴点原来的速度为点的速度的两倍，
故点原来的速度为
故答案为；
（2）设经过xs相遇，
依题意得
解得x=s
故答案为；
（3）依题意知Q点经过秒到达E点，
故经过的路程为
×=
∵AB=4，
∴-4=
＜8
E点在AD上，DE=8-=
DE×CD=××4=
故答案为：AD; ；
（4）∵每次相遇移动的时间为t=
∴Q点移动99次后的路程为99××=
÷24=
=
故Q点移动25圈，
又
=
-4=＜8
∴Q点移动99次后与P点相遇在AD上，且距离A点处.
暑假衔接教材期末暑假预习武汉出版社系列答案
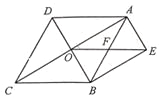
假期作业暑假成长乐园新疆青少年出版社系列答案
【题目】如图，菱形ABCD的对角线AC、BD相交于点O，BE∥AC，AE∥BD，OE与AB交于点F.
（1）试判断四边形AEBO的形状，并说明理由；
（2）若OE=10，AC=16，求菱形ABCD的面积.
【题目】某次数学单元测试，七年级第一小组共10名同学，小组长把超过班级平均分的部分记为“＋”，不足的部分记为“－”，记录如表：
与平均分的差值（分) | －15 | －9 | 0 | ＋3 | ＋12 | ＋17 |
人数 | 1 | 2 | 1 | 2 | 3 | 1 |
根据表格数据解答下列问题：
（1）第一小组同学的平均分比班级平均分高还是低?高或低多少分?
（2）若该班这次测试的平均分为80分，求第一小组10名同学的总分．
