题目内容
 有两条公路OM、ON相交成30°,沿公路OM方向,距O点80米处有一所小学A,当拖拉机沿ON方向行驶时,路两旁50米内会受到噪音的影响,已知拖拉机的速度为每小时18千米,那么拖拉机沿ON方向行驶将给小学带来噪音影响的时间为________秒.
有两条公路OM、ON相交成30°,沿公路OM方向,距O点80米处有一所小学A,当拖拉机沿ON方向行驶时,路两旁50米内会受到噪音的影响,已知拖拉机的速度为每小时18千米,那么拖拉机沿ON方向行驶将给小学带来噪音影响的时间为________秒.
12
分析:以A为圆心,以50米为半径作⊙A,交ON于B,C,过A作AD⊥ON于D;连AB;则BD=DC,AB=50米,又∠AOC=30°,OA=80,得到AD= OA=40,再在Rt△ADB中,利用勾股定理求出BD=30,从而BC=60,然后把拖拉机的速度为每小时18千米化为每秒5米,最后用路程除以速度即可得到影响的时间.
OA=40,再在Rt△ADB中,利用勾股定理求出BD=30,从而BC=60,然后把拖拉机的速度为每小时18千米化为每秒5米,最后用路程除以速度即可得到影响的时间.
解答: 解:以A为圆心,以50米为半径作⊙A,交ON于B,C,过A作AD⊥ON于D;连AB,如图,
解:以A为圆心,以50米为半径作⊙A,交ON于B,C,过A作AD⊥ON于D;连AB,如图,
根据题意,拖拉机沿ON方向行驶,在BC段对小学带来噪音影响.
由作法得BD=DC,AB=50米,
∵∠AOC=30°,OA=80,
∴AD= OA=40,
OA=40,
在Rt△ADB中,AB2=AD2+BD2,
∴BD= =30,
=30,
∴BC=2BD=60(米),
而拖拉机的速度为每小时18千米,即每秒5米,
拖拉机沿ON方向行驶将给小学带来噪音影响的时间= =12(秒).
=12(秒).
故答案为:12.
点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理.
分析:以A为圆心,以50米为半径作⊙A,交ON于B,C,过A作AD⊥ON于D;连AB;则BD=DC,AB=50米,又∠AOC=30°,OA=80,得到AD=
 OA=40,再在Rt△ADB中,利用勾股定理求出BD=30,从而BC=60,然后把拖拉机的速度为每小时18千米化为每秒5米,最后用路程除以速度即可得到影响的时间.
OA=40,再在Rt△ADB中,利用勾股定理求出BD=30,从而BC=60,然后把拖拉机的速度为每小时18千米化为每秒5米,最后用路程除以速度即可得到影响的时间.解答:
 解:以A为圆心,以50米为半径作⊙A,交ON于B,C,过A作AD⊥ON于D;连AB,如图,
解:以A为圆心,以50米为半径作⊙A,交ON于B,C,过A作AD⊥ON于D;连AB,如图,根据题意,拖拉机沿ON方向行驶,在BC段对小学带来噪音影响.
由作法得BD=DC,AB=50米,
∵∠AOC=30°,OA=80,
∴AD=
 OA=40,
OA=40,在Rt△ADB中,AB2=AD2+BD2,
∴BD=
 =30,
=30,∴BC=2BD=60(米),
而拖拉机的速度为每小时18千米,即每秒5米,
拖拉机沿ON方向行驶将给小学带来噪音影响的时间=
 =12(秒).
=12(秒).故答案为:12.
点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理.

练习册系列答案
相关题目
 有两条公路OM、ON相交成30°,沿公路OM方向,距O点80米处有一所小学A,当拖拉机沿ON方向行驶时,路两旁50米内会受到噪音的影响,已知拖拉机的速度为每小时18千米,那么拖拉机沿ON方向行驶将给小学带来噪音影响的时间为
有两条公路OM、ON相交成30°,沿公路OM方向,距O点80米处有一所小学A,当拖拉机沿ON方向行驶时,路两旁50米内会受到噪音的影响,已知拖拉机的速度为每小时18千米,那么拖拉机沿ON方向行驶将给小学带来噪音影响的时间为

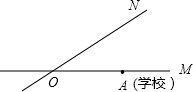 如图,有两条公路OM,ON相交成30°,沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学,当拖拉机沿ON方向行驶时,路两旁50米内会受到噪音影响,已知有两台相距30米的拖拉机正沿ON方向行驶,它们的速度均为5米/秒,问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是多少?
如图,有两条公路OM,ON相交成30°,沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学,当拖拉机沿ON方向行驶时,路两旁50米内会受到噪音影响,已知有两台相距30米的拖拉机正沿ON方向行驶,它们的速度均为5米/秒,问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是多少?