��Ŀ����
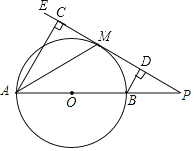
����Ŀ����֪������y��ax2+2x��![]() ��a��0����y�ύ�ڵ�A����x���һ������ΪB��
��a��0����y�ύ�ڵ�A����x���һ������ΪB��
��1������ֱ��д����A�������� ����
���������ߵĶԳ���Ϊֱ��x����4ʱ����ֱ��д��a���� ����
��2������BΪ��3��0������m2+2m+3��x��m2+2m+5����am��0ʱ����������͵��������Ϊ��![]() ����m��ֵ��
����m��ֵ��
��3����֪��C����5����3���͵�D��5��1���������������߶�CD��������ͬ�Ľ��㣬��a��ȡֵ��Χ��
���𰸡���1����![]() ����
����![]() ����2��
����2��![]() ����3��a��
����3��a��![]() ��a����3��
��a����3��
��������
��1������x��0���������ߵĽ���ʽ���y��ֵ����ɵ�A�����ꣻ
�����������ߵĶԳ��ṫʽ�г�a�ķ��̣�������a��ֵ��
��2����B��������������ߵĽ���ʽ��������a��ֵ���ٽ����֪����am��0����m��ȡֵ��Χ���ٸ��ݶ��κ��������ʽ��������m2+2m+3��x��m2+2m+5ʱ����������͵��������Ϊ![]() ,�г�m�ķ��̣����m��ֵ�������ó�m��ȷֵ��
,�г�m�ķ��̣����m��ֵ�������ó�m��ȷֵ��
��3���ô���ϵ�������CD�Ľ���ʽ������������ߵĶԳ���![]() �������������������a��0ʱ�������ߵĶ�����y����ߣ�Ҫʹ���������߶�CD��������ͬ�Ľ��㣬��C��D���������������Ϸ���������CD�·���������һ�����г�a����ʽ�飬���н�𣻵�a��0ʱ�������ߵĶ�����y����ұߣ�Ҫʹ���������߶�CD��������ͬ�Ľ��㣬��C��D���������������·��������ߵĶ��������CD�Ϸ����ݴ��г�a�IJ���ʽ����н��
�������������������a��0ʱ�������ߵĶ�����y����ߣ�Ҫʹ���������߶�CD��������ͬ�Ľ��㣬��C��D���������������Ϸ���������CD�·���������һ�����г�a����ʽ�飬���н�𣻵�a��0ʱ�������ߵĶ�����y����ұߣ�Ҫʹ���������߶�CD��������ͬ�Ľ��㣬��C��D���������������·��������ߵĶ��������CD�Ϸ����ݴ��г�a�IJ���ʽ����н��
��1������x��0����![]() ��
��
��![]() ,
,
�ʴ�Ϊ��![]() ��
��
���������ߵĶԳ���Ϊֱ��x����4��
�� ![]() ��
��
��a��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2���ߵ�BΪ��3��0����
��9a+6��![]() ��0��
��0��
��a����![]() ��
��
�������ߵĽ���ʽΪ��![]() ��
��
��Գ���Ϊx����2��
��am��0��
��m��0��
��m2+2m+3��3����2��
�ߵ�m2+2m+3��x��m2+2m+5ʱ��y��x���������С��
�ߵ�m2+2m+3��x��m2+2m+5����am��0ʱ����������͵��������Ϊ��![]() ��
��
�� ![]() ��
��
�����ã�m2+2m+5��2��4��m2+2m+5����12��0��
��ã�m2+2m+5��6����m2+2m+5����2������0���⣩��
��![]() ��
��
��m��0��
��![]() ��
��
��3����ֱ��CD�Ľ���ʽΪy��kx+b��k��0����
�ߵ�C����5����3���͵�D��5��1����
�� ![]() ��
��
��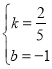 ��
��
��CD�Ľ���ʽΪ![]() ��
��
��y��ax2+2x��![]() ��a��0��
��a��0��
��Գ���Ϊ![]() ��
��
����a��0ʱ��![]() ���������ߵĶ�����y����࣬
���������ߵĶ�����y����࣬
�����������߶�CD��������ͬ�Ľ��㣬
��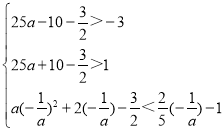 ��
��
��![]() ��
��
����a��0ʱ��![]() ���������ߵĶ�����y����࣬
���������ߵĶ�����y����࣬
�����������߶�CD��������ͬ�Ľ��㣬
��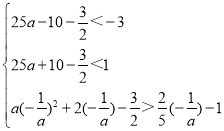 ��
��
��a����3��
���ϣ�![]() ��a����3��
��a����3��

����Ŀ������4��23�գ��ǵ�16����������գ�ijУΪ�˽�ѧ��ÿ�ܿ��������Ķ���ʱ�䣬�ڱ�У�����ȡ������ѧ�������ʾ����飬�ֽ����������Ƴ���ͼ��������ͳ��ͼ���������ͼ���е���Ϣ�����������
��� | ѧϰʱ��x��h�� | Ƶ���������� |
A | 0��x��1 | 8 |
B | 1��x��2 | 24 |
C | 2��x��3 | 32 |
D | 3��x��4 | n |
E | 4Сʱ���� | 4 |

��1�����е�n���� ������λ�������� ���飬����ͳ��ͼ��B���Ӧ��Բ�Ľ�Ϊ�� ������
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3����У���ٿ����ÿ���ʱ����������Ķ��Ľ����ᣬ�ƻ���E��ѧ�������ѡ�����˽��о�����ܣ���֪E�������ѧ���У��ߡ����꼶����1�ˣ����꼶��2�ˣ����û���״ͼ�����б������ȡ������ѧ�������Ծ��꼶�ĸ��ʣ�