题目内容
将矩形ABCD沿AE折叠,使点D落在D′处,已知∠CED′=60°,DE=1,则DD′的长为( )
A.

B.

C.2

D.3
【答案】分析:首先根据翻折变换的性质得出∠1=∠2,∠DEA=∠D′EA,利用∠CED′=60°得出∠1=∠2=30°,再利用三角函数关系求出AD的长,再利用等边三角形的判定得出DD′的长.
解答: 解:∵将矩形ABCD沿AE折叠,使点D落在D′处,已知∠CED′=60°,
解:∵将矩形ABCD沿AE折叠,使点D落在D′处,已知∠CED′=60°,
∴∠1=∠2,∠DEA=∠D′EA,∠DED′=180°-60°=120°,
∴∠DEA=∠D′EA=60°,
∴∠1=∠2=30°,
∵DE=1,
∴AD=DE÷tan30°= ,
,
∵AD=AD′,∠DAD′=30°+30°=60°,
∴△ADD′是等边三角形,
∴DD′=AD=AD′= ,
,
故选:B.
点评:此题主要考查了翻折变换的性质以及等边三角形的判定等知识,根据已知得出△ADD′是等边三角形是解题关键.
解答:
 解:∵将矩形ABCD沿AE折叠,使点D落在D′处,已知∠CED′=60°,
解:∵将矩形ABCD沿AE折叠,使点D落在D′处,已知∠CED′=60°,∴∠1=∠2,∠DEA=∠D′EA,∠DED′=180°-60°=120°,
∴∠DEA=∠D′EA=60°,
∴∠1=∠2=30°,
∵DE=1,
∴AD=DE÷tan30°=
 ,
,∵AD=AD′,∠DAD′=30°+30°=60°,
∴△ADD′是等边三角形,
∴DD′=AD=AD′=
 ,
,故选:B.
点评:此题主要考查了翻折变换的性质以及等边三角形的判定等知识,根据已知得出△ADD′是等边三角形是解题关键.

练习册系列答案
相关题目
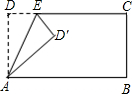 将矩形ABCD沿AE折叠,得到如图所示的图形,已知∠CED′=60°,则∠AED的大小是( )
将矩形ABCD沿AE折叠,得到如图所示的图形,已知∠CED′=60°,则∠AED的大小是( )| A、60° | B、50° | C、75° | D、55° |
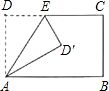 如图将矩形ABCD沿AE折叠,得到如图所示的图形,已知∠CED′=55°,则∠BAD′的大小是
如图将矩形ABCD沿AE折叠,得到如图所示的图形,已知∠CED′=55°,则∠BAD′的大小是 将矩形ABCD沿AE折叠,得到如图所示的图形,已知∠CED′=60°,则∠EAB的大小是( )
将矩形ABCD沿AE折叠,得到如图所示的图形,已知∠CED′=60°,则∠EAB的大小是( )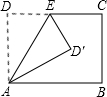 如图,将矩形ABCD沿AE折叠,若∠BAD′=30°,求∠AED′的度数.
如图,将矩形ABCD沿AE折叠,若∠BAD′=30°,求∠AED′的度数.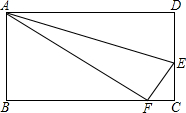 如图,将矩形ABCD沿AE折叠,使点D落在BC边上的F处,已知AB=6,BC=10,则EC=
如图,将矩形ABCD沿AE折叠,使点D落在BC边上的F处,已知AB=6,BC=10,则EC=