题目内容
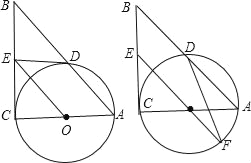
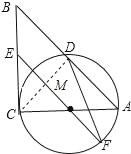
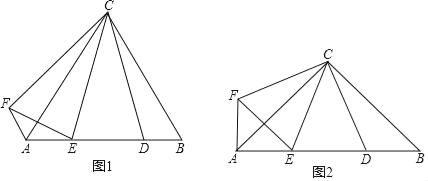
如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为 ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
【答案】(1)证明见解析;(2)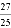
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得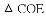
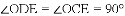
(2)连接CD,根据直径所对的圆周角是直角,即可得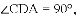
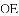
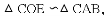
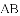
试题解析:(1)证明:连接OD,
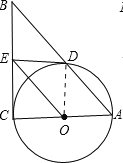
∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
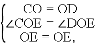 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
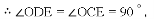
∴ED⊥OD,
∴ED是
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
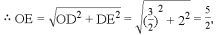
∵OE∥AB,
∴△COE∽△CAB,
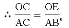 ∴AB=5,
∴AB=5,
∵AC是直径,
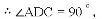
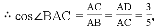
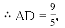
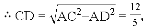
∵EF∥AB,
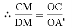
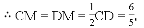
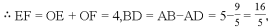
∴S△ADF=S梯形ABEF?S梯形DBEF
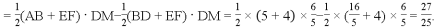
∴△ADF的面积为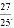
【题型】解答题
【结束】
23
某商店准备进一批季节性小家电,每个进价为40元,经市场预测,销售定价为50元,可售出400个;定价每增加1元,销售量将减少10个.设每个定价增加x元.
(1)写出售出一个可获得的利润是多少元(用含x的代数式表示)?
(2)商店若准备获得利润6000元,并且使进货量较少,则每个定价为多少元?应进货多少个?
(3)商店若要获得最大利润,则每个应定价多少元?获得的最大利润是多少?
练习册系列答案
相关题目


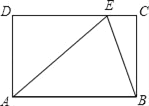
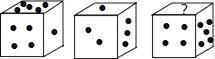
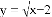 ,则x取值范围是_____.
,则x取值范围是_____.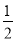 )﹣2﹣2sin60°+
)﹣2﹣2sin60°+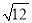 ;
;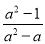 ÷(2+
÷(2+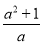 ),其中a=
),其中a=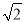 .
.