题目内容
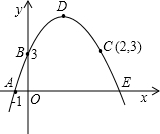
推理运算:抛物线经过A、B、C三点,顶点为D,且与x轴的另一个交点为E.
(1)求该抛物线的解析式;
(2)求四边形ABDE的面积;
(3)求证:△BDE为直角三角形;
(4)求证:△AOB∽△BDE.
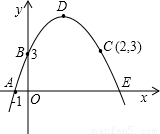
【答案】分析:(1)根据图象给出的信息,即可得到A、B、C三点的坐标,用待定系数法即可求出抛物线的解析式;
(2)根据抛物线的解析式,易求得顶点D的坐标;由于四边形ABDE不规则,可将其面积转化为其他规则图形面积的和差;过D作DF⊥x轴于F,那么四边形ABDE的面积可由△AOB、△DEF、梯形BOFD的面积和求得;
(3)根据B、D、E三点坐标,可分别求出BD、DE、BE的长,进而由勾股定理来判定△BDE是否为直角三角形;
(4)在(3)中,已证得∠BDE=90°,那么可以看所求的两个三角形的对应直角边是否成比例即可.
解答:(1)解:由图知:A(-1,0),B(0,3),C(2,3);
设抛物线的解析式为y=ax2+bx+c,则有:
 ,
,
解得 ;
;
∴抛物线的解析式为:y=-x2+2x+3=-(x-1)2+4;
(2)解:过D作DF⊥x轴于F;
由(1)的抛物线易得:D(1,4),E(3,0);
则OF=1,DF=4,EF=2;
∴S四边形ABDE=S△AOB+S△DEF+S梯形BOFD= ×1×3+
×1×3+ ×2×4+
×2×4+ ×(3+4)×1=9;
×(3+4)×1=9;
(3)证明:∵B(0,3),D(1,4),E(3,0),
∴BD2=2,DE2=20,BE2=18;
∴BD2+BE2=DE2,
故△BDE是直角三角形,且∠BDE=90°;
(4)证明:由(3)知:BD= ,DE=3
,DE=3 ;
;
∴OA:OB=BD:DE=1:3;
又∵∠AOB=∠BDE=90°;
∴△AOB∽△BDE.
点评:此题考查了二次函数解析式的确定、图形面积的求法、直角三角形的判定、勾股定理、相似三角形的判定等知识,要求学生熟练掌握这些基础知识.
(2)根据抛物线的解析式,易求得顶点D的坐标;由于四边形ABDE不规则,可将其面积转化为其他规则图形面积的和差;过D作DF⊥x轴于F,那么四边形ABDE的面积可由△AOB、△DEF、梯形BOFD的面积和求得;
(3)根据B、D、E三点坐标,可分别求出BD、DE、BE的长,进而由勾股定理来判定△BDE是否为直角三角形;
(4)在(3)中,已证得∠BDE=90°,那么可以看所求的两个三角形的对应直角边是否成比例即可.
解答:(1)解:由图知:A(-1,0),B(0,3),C(2,3);
设抛物线的解析式为y=ax2+bx+c,则有:
 ,
,解得
 ;
;∴抛物线的解析式为:y=-x2+2x+3=-(x-1)2+4;
(2)解:过D作DF⊥x轴于F;

由(1)的抛物线易得:D(1,4),E(3,0);
则OF=1,DF=4,EF=2;
∴S四边形ABDE=S△AOB+S△DEF+S梯形BOFD=
 ×1×3+
×1×3+ ×2×4+
×2×4+ ×(3+4)×1=9;
×(3+4)×1=9;(3)证明:∵B(0,3),D(1,4),E(3,0),
∴BD2=2,DE2=20,BE2=18;
∴BD2+BE2=DE2,
故△BDE是直角三角形,且∠BDE=90°;
(4)证明:由(3)知:BD=
 ,DE=3
,DE=3 ;
;∴OA:OB=BD:DE=1:3;
又∵∠AOB=∠BDE=90°;
∴△AOB∽△BDE.
点评:此题考查了二次函数解析式的确定、图形面积的求法、直角三角形的判定、勾股定理、相似三角形的判定等知识,要求学生熟练掌握这些基础知识.

练习册系列答案
相关题目
 推理运算:
推理运算: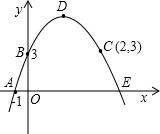 推理运算:
推理运算: