题目内容
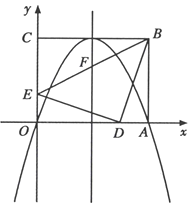
【题目】将一副三角板![]() 与
与![]() (其中
(其中![]() ,
,![]() ,
,![]() ,
,![]() )如图摆放,
)如图摆放,![]() 中
中![]() 所对直角边与
所对直角边与![]() 斜边恰好重合.以
斜边恰好重合.以![]() 为直径的圆经过点
为直径的圆经过点![]() ,且与
,且与![]() 交于点
交于点![]() ,分别连接
,分别连接![]() ,
,![]() .
.
(1)求证:![]() 平分
平分![]() ;
;
(2)求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)由Rt△ACB中∠ABC=45°,得出∠BAC=∠ABC=45°,根据圆周角定理得出∠AEC=∠ABC,∠BEC=∠BAC,等量代换得出∠AEC=∠BEC,即EC平分∠AEB;
(2)设AB与CE交于点M.根据角平分线的性质得出![]() .易求∠BAD=30°,由直径所对的圆周角是直角得出∠AEB=90°,解直角△ABE得到AE=
.易求∠BAD=30°,由直径所对的圆周角是直角得出∠AEB=90°,解直角△ABE得到AE=![]() BE,那么
BE,那么![]()
![]() .作AF⊥CE于F,BG⊥CE于G.证明△AFM∽△BGM,根据相似三角形对应边成比例得出
.作AF⊥CE于F,BG⊥CE于G.证明△AFM∽△BGM,根据相似三角形对应边成比例得出![]() ,进而求出
,进而求出 .
.
试题解析:(1)证明:∵Rt△ACB中,∠ACB=90°,∠ABC=45°,
∴∠BAC=∠ABC=45°,
∵∠AEC=∠ABC,∠BEC=∠BAC,∴∠AEC=∠BEC,
即EC平分∠AEB;
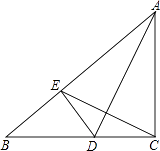
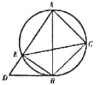
(2)如图,设AB与CE交于点M.
∵EC平分∠AEB,∴![]() .
.
在Rt△ABD中,∠ABD=90°,∠D=60°,
∴∠BAD=30°,
∵以AB为直径的圆经过点E,∴∠AEB=90°,
∴tan∠BAE=![]() ,∴AE=
,∴AE=![]() BE,∴
BE,∴![]() =
=![]() .
.
作AF⊥CE于F,BG⊥CE于G.
在△AFM与△BGM中,
∵∠AFM=∠BGM=90°,∠AMF=∠BMG,∴△AFM∽△BGM,
∴![]() ,∴
,∴ .
.


练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目