题目内容
在8×8的正方形网格中建立如图所示的平面直角坐标系,已知![]() 是第一象限内的一个格点,由点
是第一象限内的一个格点,由点![]() 与线段
与线段![]() 组成一个以
组成一个以![]() 为底,且腰长为无理数的等腰三角形.
为底,且腰长为无理数的等腰三角形.
(1)求点![]() 的坐标及△
的坐标及△![]() 的面积.
的面积.
(2)请探究:在![]() 轴上是否存在这样的点
轴上是否存在这样的点![]() ,使以
,使以![]() 为顶点的四边形的面积等于△
为顶点的四边形的面积等于△![]() 面
面![]() 积的2
积的2![]() 倍?若存在,请写出点
倍?若存在,请写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

|
解![]() :(1)分析可知点
:(1)分析可知点![]() 应在
应在![]() 的垂直平分线上,又在第一象限,且腰长是无理数,只有点(1,1)满足.即C(1,1).
的垂直平分线上,又在第一象限,且腰长是无理数,只有点(1,1)满足.即C(1,1).
如图,△![]() 的面积可由梯形
的面积可由梯形![]() 的面积加上△
的面积加上△![]() 的面积减去△
的面积减去△![]() 的面积
的面积![]() 得到,
得到,![]() .
.
(2)因为△![]() 的面积是4,故以
的面积是4,故以![]() 为顶点的四边形的面积应为8.
为顶点的四边形的面积应为8.
同(1)中的方法得到![]() 三点构成的三角形面积为6.
三点构成的三角形面积为6.
若![]() 点在
点在![]() 点左边,△
点左边,△![]() 的面积应为2,高为4,那么底边长为1,
的面积应为2,高为4,那么底边长为1,
此时![]() 点坐标为(-1,0);
点坐标为(-1,0);
若![]() 点在
点在![]() 点右边,△
点右边,△![]() 的面积应为2,高为2,所以底边长为2,
的面积应为2,高为2,所以底边长为2,
此时![]() 点坐标为(2,0).
点坐标为(2,0).
故点![]() 的坐标为(2,0)或(-1,0).
的坐标为(2,0)或(-1,0).

|

练习册系列答案
相关题目
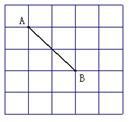
 (2011•岳池县模拟)在6×8的正方形网格中建立了如图所示的平面直角坐标系xoy,已知每个最小正方形边长为1,将图中的OA绕O点逆时针旋转90°得到OA′,则A′点坐标为
(2011•岳池县模拟)在6×8的正方形网格中建立了如图所示的平面直角坐标系xoy,已知每个最小正方形边长为1,将图中的OA绕O点逆时针旋转90°得到OA′,则A′点坐标为 如图,在10×10的正方形网格纸中(每个小方格的边长都是1个单位)有一个△ABC,请在网格纸中画出以点O为旋转中心把△ABC按顺时针方向旋转90°得到的△A′B′C′.
如图,在10×10的正方形网格纸中(每个小方格的边长都是1个单位)有一个△ABC,请在网格纸中画出以点O为旋转中心把△ABC按顺时针方向旋转90°得到的△A′B′C′.