题目内容
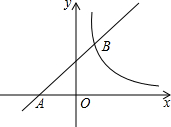 如图已知直线y=kx+b与x轴交于A点,且与函数y=
如图已知直线y=kx+b与x轴交于A点,且与函数y=| m |
| x |
| m |
| x |
分析:把y=0代入函数y=kx+2求出直线与x轴的交点的横坐标,得出0≤kx+2的解集,求出两函数在第一象限内的交点的横坐标,即可得出不等式kx+2<
的解集,最后求出答案即可.
| m |
| x |
解答:解:∵从函数y=kx+b的图象可知:k>0,
∴把y=0代入函数y=kx+2得:0=kx+2,
∴x=-
,
即直线y=kx+2与x轴的交点坐标是(-
,0),
∴不等式0≤kx+2的解集是x≥-
,
把y=
代入y=kx+2整理得:kx2+2x-m=0,
解得:x=
,x2=
,
∵从函数y=kx+b的图象可知:k>0,
∴函数y=kx+2和函数y=
在第一象限的交点的横坐标是
,
∴不等式组0≤kx+2<
的解集是0≤x<
.
∴把y=0代入函数y=kx+2得:0=kx+2,
∴x=-
| 2 |
| k |
即直线y=kx+2与x轴的交点坐标是(-
| 2 |
| k |
∴不等式0≤kx+2的解集是x≥-
| 2 |
| k |
把y=
| m |
| x |
解得:x=
-1+
| ||
| k |
-1-
| ||
| k |
∵从函数y=kx+b的图象可知:k>0,
∴函数y=kx+2和函数y=
| m |
| x |
-1+
| ||
| k |
∴不等式组0≤kx+2<
| m |
| x |
-1+
| ||
| k |
点评:本题考查了一次函数与反比例函数的交点问题的应用,主要考查学生观察图形的能力和计算能力,题目比较好,但是有一定的难度.

练习册系列答案
相关题目
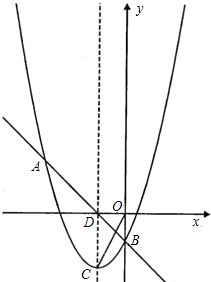 点,抛物线的顶点为C(-1,-2),对称轴交直线AB于点D,连接OC.
点,抛物线的顶点为C(-1,-2),对称轴交直线AB于点D,连接OC.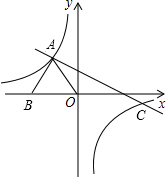 如图已知,△OAB中,AB=AO=5,OB=6,双曲线
如图已知,△OAB中,AB=AO=5,OB=6,双曲线 如图已知直线y=kx+b与x轴交于A点,且与函数
如图已知直线y=kx+b与x轴交于A点,且与函数 在第一象限的图象交于B点,求不等式组
在第一象限的图象交于B点,求不等式组 的解集.
的解集. 在第一象限的图象交于B点,求不等式组
在第一象限的图象交于B点,求不等式组 的解集.
的解集.