题目内容
(2012•金东区一模)如图,正方形ABCD,矩形EFGH均位于第一象限内,它们的边平行于x轴或y轴,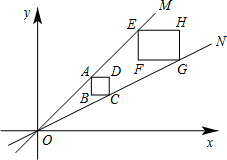 其中,点A,E在直线OM上,点C,G在直线ON上,O为坐标原点,点A的坐标为(3,3),正方形ABCD的边长为1.
其中,点A,E在直线OM上,点C,G在直线ON上,O为坐标原点,点A的坐标为(3,3),正方形ABCD的边长为1.
(1)直线ON的解析式是
(2)若矩形EFGH的周长为10,面积为6,则点F的坐标为
 其中,点A,E在直线OM上,点C,G在直线ON上,O为坐标原点,点A的坐标为(3,3),正方形ABCD的边长为1.
其中,点A,E在直线OM上,点C,G在直线ON上,O为坐标原点,点A的坐标为(3,3),正方形ABCD的边长为1.(1)直线ON的解析式是
y=
x
| 1 |
| 2 |
y=
x
;| 1 |
| 2 |
(2)若矩形EFGH的周长为10,面积为6,则点F的坐标为
(7,5)或(8,5)
(7,5)或(8,5)
.分析:(1)先根据A的坐标为(3,3),正方形ABCD的边长为1得出直线OM的解析式,再求出C点的坐标利用待定系数法即可求出直线ON的解析式;
(2)设矩形EFGH的宽为a,则长为5-a,再根据面积为6即可得出a的值,由点E在直线OM上设点E的坐标为(e,e),由矩形的边长可用e表示出F、G点的坐标,再根据G点在直线ON上即可得出e的值,进而得出结论.
(2)设矩形EFGH的宽为a,则长为5-a,再根据面积为6即可得出a的值,由点E在直线OM上设点E的坐标为(e,e),由矩形的边长可用e表示出F、G点的坐标,再根据G点在直线ON上即可得出e的值,进而得出结论.
解答:解:(1)∵A的坐标为(3,3),
∴直线OM的解析式为y=x,
∵正方形ABCD的边长为1,
∴C(4,2),
设直线ON的解析式为y=kx(k≠0),
∴2=4k,解得k=
,
∴直线ON的解析式为:y=
x;
(2)设矩形EFGH的宽为a,则长为5-a,
∵矩形EFGH的面积为6,
∴a(5-a)=6,
解得a=2或a=3,
当a=2即EF=2时,EH=5-2=3,
∵点E在直线OM上,设点E的坐标为(e,e),
∴F(e,e-2),G(e+3,e-2),
∵点G在直线ON上,
∴e-2=
(e+3),解得e=7,
∴F(7,5);
当a=3即EF=3时,EH=5-3=2,
∵点E在直线OM上,设点E的坐标为(e,e),
∴F(e,e-3),G(e+2,e-3),
∵点G在直线ON上,
∴e-3=
(e+2),
解得e=8,
∴F(8,5).
故答案为:y=
x;(7,5),(8,5).
∴直线OM的解析式为y=x,
∵正方形ABCD的边长为1,
∴C(4,2),
设直线ON的解析式为y=kx(k≠0),
∴2=4k,解得k=
| 1 |
| 2 |
∴直线ON的解析式为:y=
| 1 |
| 2 |
(2)设矩形EFGH的宽为a,则长为5-a,
∵矩形EFGH的面积为6,
∴a(5-a)=6,
解得a=2或a=3,
当a=2即EF=2时,EH=5-2=3,
∵点E在直线OM上,设点E的坐标为(e,e),
∴F(e,e-2),G(e+3,e-2),
∵点G在直线ON上,
∴e-2=
| 1 |
| 2 |
∴F(7,5);
当a=3即EF=3时,EH=5-3=2,
∵点E在直线OM上,设点E的坐标为(e,e),
∴F(e,e-3),G(e+2,e-3),
∵点G在直线ON上,
∴e-3=
| 1 |
| 2 |
解得e=8,
∴F(8,5).
故答案为:y=
| 1 |
| 2 |
点评:本题考查的是一次函数综合题,根据题意得出直线ON的解析式是解答此题的关键,在解答(2)时要注意进行分类讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•金东区一模)如图,已知正方形ABCD的边长为8,以AB为直径的⊙O交对角线AC于点F,点E在⊙O上(E,F分别在直径AB的两侧).
(2012•金东区一模)如图,已知正方形ABCD的边长为8,以AB为直径的⊙O交对角线AC于点F,点E在⊙O上(E,F分别在直径AB的两侧). (2012•金东区一模)二次函数y=ax2+bx+c的图象如图所示,则下列判断中错误的是( )
(2012•金东区一模)二次函数y=ax2+bx+c的图象如图所示,则下列判断中错误的是( ) (2012•金东区一模)如图,为安全起见,幼儿园打算加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3m,点D,B,C在同一水平地面上,那么加长后的滑梯AD的长是
(2012•金东区一模)如图,为安全起见,幼儿园打算加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3m,点D,B,C在同一水平地面上,那么加长后的滑梯AD的长是