题目内容
已知△ABC的三边长分别为a、b、c，且满足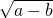
+|b-2|=0，第三边c为偶数，则△ABC的周长为________．
6
分析：先根据非负数的性质求出a、b的值，再根据三角形的三边关系及c为偶数求出c的值即可得出三角形的周长．
解答：∵△ABC的三边a，b，c满足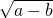+|b-2|=0，
∴b=2，a=2，
根据三角形的三边关系定理即任意两边之和＞第三边得到0＜c＜4，
∵c为偶数，
∴c=2，
∴△ABC的周长=6．
故答案为6．
点评：本题考查三角形的三边关系定理以及推论，即任意两边之和＞第三边，两边之差＜第三边．
分析：先根据非负数的性质求出a、b的值，再根据三角形的三边关系及c为偶数求出c的值即可得出三角形的周长．
解答：∵△ABC的三边a，b，c满足
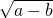+|b-2|=0，∴b=2，a=2，
根据三角形的三边关系定理即任意两边之和＞第三边得到0＜c＜4，
∵c为偶数，
∴c=2，
∴△ABC的周长=6．
故答案为6．
点评：本题考查三角形的三边关系定理以及推论，即任意两边之和＞第三边，两边之差＜第三边．
练习册系列答案
相关题目