题目内容
（2012•广西）如图，在△ABC中，已知∠A=80°，∠B=60°，DE∥BC，那么∠CED的大小是（ ）分析：先根据三角形内角和定理计算出∠C=180°-∠A-∠B=180°-80°-60°=40°，再根据平行线的性质得到∠CED+∠C=180°，即∠CED=180°-40°=140°．
解答：解：∵∠A+∠B+∠C=180°，
∴∠C=180°-∠A-∠B=180°-80°-60°=40°，
又∵DE∥BC，
∴∠CED+∠C=180°，
∴∠CED=180°-40°=140°．
故选D．
∴∠C=180°-∠A-∠B=180°-80°-60°=40°，
又∵DE∥BC，
∴∠CED+∠C=180°，
∴∠CED=180°-40°=140°．
故选D．
点评：本题考查了三角形内角和定理：三角形内角和为180°．也考查了平行线的性质．
练习册系列答案
相关题目
（2012•广西）如图，已知线段OA交⊙O于点B，且OB=AB，点P是⊙O上的一个动点，那么∠OAP的最大值是（ ）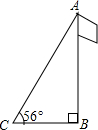
（2012•广西）如图，为测量旗杆AB的高度，在与B距离为8米的C处测得旗杆顶端A的仰角为56°，那么旗杆的高度约是
（2012•广西）如图，在?ABCD中，BE交对角线AC于点E，DF∥BE交AC于点F．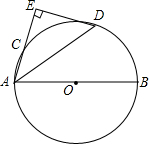
（2012•广西）如图，AB是⊙O的直径，点C是⊙O上一点，∠BAC的平分线AD交⊙O于点D，过点D垂直于AC的直线交AC的延长线于点E．