题目内容
(本小题满分12分)已知:抛物线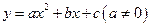 的对称轴为
的对称轴为 与
与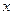 轴交于
轴交于 两点,与
两点,与 轴交于点
轴交于点 其中
其中 、
、

(1)求这条抛物线的函数表达式.
(2)已知在对称轴上存在一点P,使得
 的周长最小.请求出点P的坐标.
的周长最小.请求出点P的坐标.(3)若点
 是线段
是线段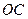 上的一个动点(不与点O、点C重合).过点D作
上的一个动点(不与点O、点C重合).过点D作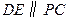 交
交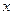 轴于点
轴于点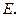 连接
连接 、
、 .设
.设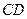 的长为
的长为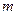 ,
,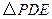 的面积为
的面积为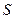 .求
.求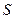 与
与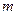 之间的函数关系式.试说明
之间的函数关系式.试说明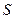 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.
是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.
解:(1)由题意得
解得
∴此抛物线的解析式为
(2)连结 、
、 .因为
.因为 的长度一定,所以
的长度一定,所以 周长最小,就是使
周长最小,就是使 最小.
最小. 点关于对称轴的对称点是
点关于对称轴的对称点是 点,
点, 与对称轴
与对称轴 的交点即为所求的点
的交点即为所求的点 .
.
 设直线
设直线 的表达式为
的表达式为 则
则 解得
解得 ∴此直线的表达式为
∴此直线的表达式为
把 代入得
代入得
∴ 点的坐标为
点的坐标为
(3)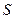 存在最大值
存在最大值
理由:∵ 即
即
∴
∴ 即
即
∴
连结

=
=
∵
∴当 时,
时, 解析:
解析:
略

解得

∴此抛物线的解析式为

(2)连结
 、
、 .因为
.因为 的长度一定,所以
的长度一定,所以 周长最小,就是使
周长最小,就是使 最小.
最小. 点关于对称轴的对称点是
点关于对称轴的对称点是 点,
点, 与对称轴
与对称轴 的交点即为所求的点
的交点即为所求的点 .
. 设直线
设直线 的表达式为
的表达式为 则
则 解得
解得 ∴此直线的表达式为
∴此直线的表达式为
把
 代入得
代入得
∴
 点的坐标为
点的坐标为
(3)
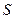 存在最大值
存在最大值理由:∵
 即
即
∴

∴
 即
即
∴

连结


=

=

∵

∴当
 时,
时, 解析:
解析:略

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 的图象经过A、B两点,根据图中信息解答下列问题:
的图象经过A、B两点,根据图中信息解答下列问题:


 同侧,在直线
同侧,在直线 ,连接
,连接 ,与直线
,与直线


