��Ŀ����
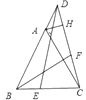
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A����Ϊ(6��0)����B��y����������ϣ��� ![]() =24 ��
=24 ��
��1�����B���ꣻ
��2������P��B������y�Ḻ���᷽���˶����ٶ�ÿ��2����λ���˶�ʱ��t�룬��AOP�����ΪS����S��t�Ĺ�ϵʽ����ֱ��д��t��ȡֵ��Χ��
��3����(2)�������£���S��AOP��S��ABP=1:3����S��AOP+S��ABP=S��AOB�����߶�AB�Ĵ�ֱƽ�������Ƿ���ڵ�Q��ʹ�á�AOQ��������BPQ�������ȣ������ڣ����Q�����ꣻ�������ڣ���˵�����ɡ�
���𰸡�
��1���⣺�ߵ� ![]() ����Ϊ
����Ϊ ![]() ��
��![]() ��
�� ![]() ��
��
�� ![]() ��
��![]() �� B��������0,8��
�� B��������0,8��
��2���⣺��0��t<4ʱ��S= ![]() ����8-2t����6=24-6t��
����8-2t����6=24-6t��
��t>4ʱ��S= ![]() ��2t-8����6=6t-24
��2t-8����6=6t-24
��3���⣺ ![]()
�߶� ![]() �Ĵ�ֱƽ���߽�
�Ĵ�ֱƽ���߽� ![]() ��
�� ![]() ,��
,�� ![]() ��
�� ![]() ��
��
�ɹ��ɶ����� ![]() ,���
,��� ![]() ������Ϊ
������Ϊ ![]()
![]() ��
�� ![]() ������Ϊ
������Ϊ ![]()
���ֱ�� ![]() �Ľ���ʽΪ
�Ľ���ʽΪ ![]()
![]()
![]() ��
�� ![]() ������Ϊ(-1,1)��7,7��
������Ϊ(-1,1)��7,7��
����������1������A�������ó�OA�ij��ȣ�Ȼ�����S��AOB�г�������⼴�ɵó�OB�ij��ȣ������ó�B������� ��
��2��������������� ���ٵ�0��t<4ʱ��S= ![]() ����8-2t����6=24-6t ���ڵ�t>4ʱ��S=
����8-2t����6=24-6t ���ڵ�t>4ʱ��S= ![]() ��2t-8����6=6t-24 ��
��2t-8����6=6t-24 ��
��3����S��AOP��S��ABP=1:3����S��AOP+S��ABP=S��AOB�ó� OP = 2 , BP = 6�����߶� ![]() �Ĵ�ֱƽ���߽�
�Ĵ�ֱƽ���߽� ![]() ��
�� ![]() ,��
,�� ![]() ��
�� ![]() ���ɹ��ɶ�����
���ɹ��ɶ����� ![]() ,���
,��� ![]() ������Ϊ
������Ϊ ![]()
![]() ��
�� ![]() ������
������![]() �ɴ���ϵ�������ֱ��
�ɴ���ϵ�������ֱ�� ![]() �Ľ���ʽΪ
�Ľ���ʽΪ ![]()
![]() �Ӷ��ó�Q������ꡣ
�Ӷ��ó�Q������ꡣ

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�