题目内容
在Rt△ABC中,∠A=90°,AC=AB=4, D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)如图1,当α=90°时,线段BD1的长等于 ,线段CE1的长等于 ;(直接填写结果)
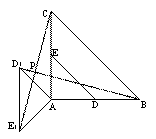
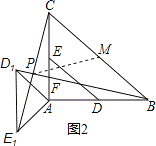
(2)如图2,当α=135°时,求证:BD1= CE1,且BD1⊥CE1;
(3)①设BC的中点为M,则线段PM的长为 ;②点P到AB所在直线的距离的最大值为 .(直接填写结果)
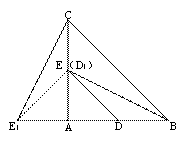
解:(1)∵∠A=90°,AC=AB=4,D,E分别是边AB,AC的中点,
∴AE=AD=2,
∵等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,设旋转角为α(0<α≤180°),
∴当α=90°时,AE1=2,∠E1AE=90°,
∴BD1=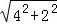 =2
=2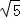 ,E1C=
,E1C=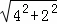 =2
=2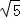 ;
;
故答案为:2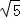 ,2
,2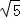 ;
;
(2)证明:当α=135°时,如图2,
∵Rt△AD1E是由Rt△ADE绕点A逆时针旋转135°得到,
∴AD1=AE1,∠D1AB=∠E1AC=135°,
在△D1AB和△E1AC中
∵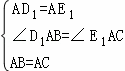 ,
,
∴△D1AB≌△E1AC(SAS),
∴BD1=CE1,且∠D1BA=∠E1CA,
记直线BD1与AC交于点F,
∴∠BFA=∠CFP,
∴∠CPF=∠FAB=90°,
∴BD1⊥CE1;
(3)解:①∵∠CPB=∠CAB=90°,BC的中点为M,
∴PM=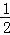 BC,
BC,
∴PM=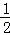
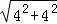 =2
=2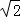 ,
,
故答案为:2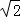 ;
;
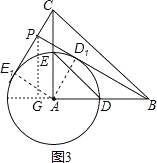
②如图3,作PG⊥AB,交AB所在直线于点G,
∵D1,E1在以A为圆心,AD为半径的圆上,
当BD1所在直线与⊙A相切时,直线BD1与CE1的交点P到直线AB的距离最大,
此时四边形AD1PE1是正方形,PD1=2,则BD1=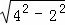 =2
=2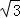 ,
,
故∠ABP=30°,
则PB=2+2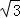 ,
,
故点P到AB所在直线的距离的最大值为:PG=1+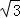 .
.
故答案为:1+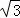 .
.

下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数 与方差
与方差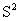 :
:
| 甲 | 乙 | 丙 | 丁 | |
| 平均数 | 561 | 560 | 561 | 560 |
| 方差 | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择
A. 甲 B.乙 C.丙 D.丁
 ∽△
∽△ 且
且 ,则
,则 为
为 化简,再求值,其中
化简,再求值,其中
 ,求代数式
,求代数式 的值.
的值.
 图象上的两个点,则m的值为________.
图象上的两个点,则m的值为________.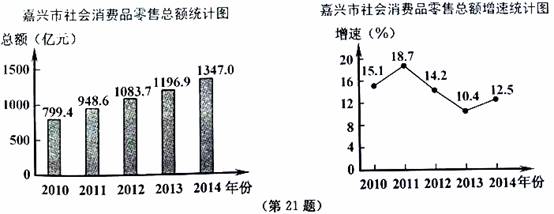 请根据图中信息,解答下列问题:
请根据图中信息,解答下列问题: