题目内容
矩形的面积为120cm2,周长为46cm,则它的对角线长为
- A.15cm
- B.16cm
- C.17cm
- D.18cm
C
分析:首先根据题意求出矩形的长与宽,然后根据勾股定理求出对角线长.
解答:设矩形长为a,宽为b.
∴ab=120;2(a+b)=46.
∴a2-23a+120=0.
∴a=15,b=8.
∴它的对角线的长为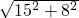 =17cm.
=17cm.
故选C.
点评:本题考查的是矩形的性质及勾股定理的运用.
分析:首先根据题意求出矩形的长与宽,然后根据勾股定理求出对角线长.
解答:设矩形长为a,宽为b.
∴ab=120;2(a+b)=46.
∴a2-23a+120=0.
∴a=15,b=8.
∴它的对角线的长为
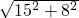 =17cm.
=17cm.故选C.
点评:本题考查的是矩形的性质及勾股定理的运用.

练习册系列答案
相关题目
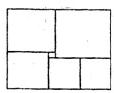 如图所示的矩形是由六个正方形组成,其中最小的正方形的面积为1,则此矩形的面积为( )
如图所示的矩形是由六个正方形组成,其中最小的正方形的面积为1,则此矩形的面积为( ) 如图所示的矩形是由六个正方形组成,其中最小的正方形的面积为1,则此矩形的面积为
如图所示的矩形是由六个正方形组成,其中最小的正方形的面积为1,则此矩形的面积为