题目内容
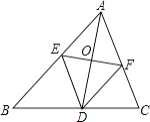
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP , 其中正确的个数是( ) 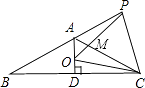
A.1
B.2
C.3
D.4
【答案】D
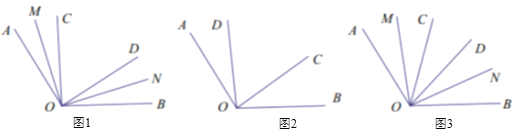
【解析】解:如图1,连接OB, 
∵AB=AC,AD⊥BC,
∴BD=CD,∠BAD= ![]() ∠BAC=
∠BAC= ![]() ×120°=60°,
×120°=60°,
∴OB=OC,∠ABC=90°﹣∠BAD=30°
∵OP=OC,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DCO=∠DBO,
∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°;
故①正确;
∵∠APC+∠DCP+∠PBC=180°,
∴∠APC+∠DCP=150°,
∵∠APO+∠DCO=30°,
∴∠OPC+∠OCP=120°,
∴∠POC=180°﹣(∠OPC+∠OCP)=60°,
∵OP=OC,
∴△OPC是等边三角形;
故②正确;
如图2,在AC上截取AE=PA,
∵∠PAE=180°﹣∠BAC=60°,
∴△APE是等边三角形,
∴∠PEA=∠APE=60°,PE=PA,
∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,
∴∠APO=∠CPE,
∵OP=CP,
在△OPA和△CPE中, ,
,
∴△OPA≌△CPE(SAS),
∴AO=CE,
∴AC=AE+CE=AO+AP;
故③正确;
如图3,过点C作CH⊥AB于H,
∵∠PAC=∠DAC=60°,AD⊥BC,
∴CH=CD,
∴S△ABC= ![]() ABCH,
ABCH,
S四边形AOCP=S△ACP+S△AOC= ![]() APCH+
APCH+ ![]() OACD=
OACD= ![]() APCH+
APCH+ ![]() OACH=
OACH= ![]() CH(AP+OA)=
CH(AP+OA)= ![]() CHAC,
CHAC,
∴S△ABC=S四边形AOCP;
故④正确.
故选D.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等,以及对等腰三角形的性质的理解,了解等腰三角形的两个底角相等(简称:等边对等角).

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】某市准备将一批帐篷和食品送往扶贫区.已知帐篷和食品共320件,且帐篷比食品多80件.
(1)直接写出帐篷有 件,食品有 件;
(2)现计划租用A、B两种货车共8辆,一次性将这批物资全部送到扶贫区,已知两种车可装帐篷和食品的件数以及每辆货车所需付运费情况如表,问:共有几种租车的方案?最少运费是多少?
帐篷(件) | 食品(件) | 每辆需付运费(元) | |
A种货车 | 40 | 10 | 780 |
B种货车 | 20 | 20 | 700 |