题目内容
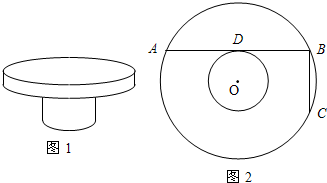
 如图所示,已知两同心圆中,大圆的弦AB,AC切小圆于D,E,△ABC的周长为12cm,求△ADE的周长.
如图所示,已知两同心圆中,大圆的弦AB,AC切小圆于D,E,△ABC的周长为12cm,求△ADE的周长.
分析:此题根据切线的性质定理和垂径定理可以得到AD=BD,AE=CE;再根据三角形的中位线定理可以得到DE=
BC,从而发现要求的三角形的周长是三角形ABC的周长的
.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:连接OD,OE;
解:连接OD,OE;
∵AB,AC切小圆于D,E,
∴OD⊥AB,OE⊥AC,
∴AD=
AB,AE=
AC,
∴DE是△ABC的中位线,
∴DE=
BC;
∵△ABC的周长=AB+AC+BC=12cm,
∴△ADE的周长=AD+AE+DE=
AB+
AC+
BC=
(AB+AC+BC)=
×12=6(cm),
故△ADE的周长为6cm.
 解:连接OD,OE;
解:连接OD,OE;∵AB,AC切小圆于D,E,
∴OD⊥AB,OE⊥AC,
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
∴DE是△ABC的中位线,
∴DE=
| 1 |
| 2 |
∵△ABC的周长=AB+AC+BC=12cm,
∴△ADE的周长=AD+AE+DE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故△ADE的周长为6cm.
点评:连接过切点的半径是圆中常见的辅助线,进一步结合垂径定理发现相等线段.掌握三角形的中位线定理.

练习册系列答案
相关题目