��Ŀ����
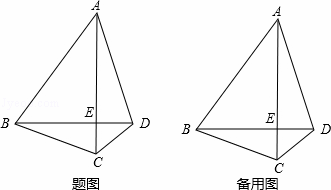
��ͼ�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�E����AC��BD����ADB=��CAD+��ABD����BAD=3��CBD��
��1����֤����ABCΪ���������Σ�
��2��M���߶�BD��һ�㣬BM��AB=3��4����F��BA���ӳ����ϣ�����FM����BFM��ƽ����FN��BD�ڵ�N����AD�ڵ�G����HΪBF�е㣬����MH����GN=GDʱ��̽���߶�CD��FM��MH֮���������ϵ����֤����Ľ��ۣ�
��1��֤������ͼ1������BAP=��DAE=�£�AP��BD��P��
���CBD=������CAD=�£�
�ߡ�ADB=��CAD+��ABD����APE=��BAP+��ABD��
���APE=��ADE��AP=AD��
��AC��BD
���PAE=��DAE=�£�
���PAD=2�£���BAD=3�£�
�ߡ�BAD=3��CBD��
��3��=3������=����
��AC��BD��
���ACB=90�㩁��CBE=90�㩁��=90�㩁�£�
�ߡ�ABC=180�㩁��BAC����ACB=90�㩁�£�
���ACB=��ABC��
���ABC����������
��2��2MH=FM+ CD��
CD��
֤������ͼ2��
�ɣ�1��֪AP=AD��AB=AC����BAP=��CAD=�£�
���ABP�ס�ACD��
���ABE=��ACD��
��AC��BD��
���GDN=90�㩁�£�
��GN=GD��
���GND=��GDN=90�㩁�£�
���NGD=180�㩁��GND����GDN=2�£�
���AGF=��NGD=2�£�
���AFG=��BAD����AGF=3�©�2��=�£�
��FNƽ�֡�BFM��
���NFM=��AFG=�£�
��FM��AE��
���FMN=90�㣮
��HΪBF���е㣬
��BF=2MH��
��FB�Ͻ�ȡFR=FM������RM��
���FRM=��FMR=90�㩁�£�
�ߡ�ABC=90�㩁�£�
���FRM=��ABC��
��RM��BC��
���CBD=��RMB��
�ߡ�CAD=��CBD=�£�
���RMB=��CAD��
�ߡ�RBM=��ACD��
���RMB�ס�DAC��
�� ��
��
��BR= CD��
CD��
��BR=BF��FR��
��FB��FM=BR= CD��
CD��
FB=FM+ CD��
CD��
��2MH=FM+ CD��
CD��



 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д���һ����n���ε�ÿ���ڽ�Ϊ156�㣬�������n���εı����ǣ�������
| �� | A�� | 13 | B�� | 14 | C�� | 15 | D�� | 16 |
һԪһ�β���ʽx��1��0�Ľ⼯�������ϱ�ʾ��ȷ���ǣ�������
| �� | A�� |
| B�� |
| C�� |
| D�� |
|
 ������ABC�Ƶ�P��ת180�㣬�õ���MCB��
������ABC�Ƶ�P��ת180�㣬�õ���MCB��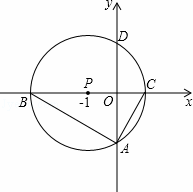


 B��
B��  C��
C��  D��
D�� 

 =
= B��
B��  =
= C��
C��  =
= D��
D��  =
=




