题目内容
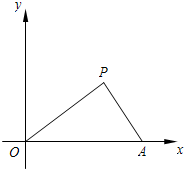 (2007•上海模拟)已知:如图,在△OAP中,OA=6,sin∠POA=
(2007•上海模拟)已知:如图,在△OAP中,OA=6,sin∠POA=| 3 |
| 5 |
| 2 |
| 3 |
(1)求点P的坐标;
(2)求二次函数的解析式;
(3)在x轴的下方,且在二次函数图象的对称轴上求一点M,使得△MOP与△AOP的面积相等.
分析:(1)过点P作PH⊥OA,垂足为点H,将原图分为两个直角三角形,利用锐角三角函数的定义,列方程求解;
(2)设所求二次函数的解析式为y=ax2+bx+c,由O、A、P三点坐标代入,列方程求a、b、c的值,确定抛物线解析式;
(3)根据二次函数解析式可知,对称轴为x=3,可设点M的坐标为(3,y),二次函数的对称轴与OP相交于点C,由P点坐标可求直线OP解析式,把x=3代入可求C点坐标,由S△MOP=S△COM+S△PCM,S△MOP=S△AOP,列方程求M点纵坐标y即可.
(2)设所求二次函数的解析式为y=ax2+bx+c,由O、A、P三点坐标代入,列方程求a、b、c的值,确定抛物线解析式;
(3)根据二次函数解析式可知,对称轴为x=3,可设点M的坐标为(3,y),二次函数的对称轴与OP相交于点C,由P点坐标可求直线OP解析式,把x=3代入可求C点坐标,由S△MOP=S△COM+S△PCM,S△MOP=S△AOP,列方程求M点纵坐标y即可.
解答:解:(1)过点P作PH⊥OA,垂足为点H.
设点P的坐标为(x,y),则OH=x,PH=y. (1分)
∵sin∠POA=
,∴tan∠POA=
.∴
=
.∴OH=
y. (1分)
∵cot∠PAO=
,∴
=
.∴AH=
y. (1分)
∵OA=OH+AH=6,∴
y+
y=6. (1分)
∴y=3.∴x=4.
∴点P的坐标为(4,3). (1分)
(2)设所求二次函数的解析式为y=ax2+bx+c.
由题意,得
(1分)
解得
(1分)
∴所求二次函数的解析式为y=-
x2+
x. (1分)
(3)设点M的坐标为(3,y),二次函数的对称轴与OP相交于点C.
由题意,得 点C的坐标为(3,
). (1分)
∴S△MOP=S△COM+S△PCM=
(
-y)×3+
(
-y)×1=
(
-y)×4=2(
-y).
(1分)
而S△MOP=S△AOP,S△AOP=
×6×3=9,(1分)
∴2(
-y)=9.∴y=-
.
∴点M的坐标为(3,-
). (1分)
另解:设二次函数的对称轴与x轴交于点B,连接MA.
∵△MOP与△AOP的面积相等,且OP是公共边,
∴点M到OP与点A到OP的距离相等. (1分)
∴AM∥OP.
∴∠MAB=∠POA.(1分)
∴tan∠MAB=tan∠POA=
.
∵AB=3,∴
=
. (1分)
∴BM=
.
∴点M的坐标为(3,-
). (1分)
设点P的坐标为(x,y),则OH=x,PH=y. (1分)
∵sin∠POA=
| 3 |
| 5 |
| 3 |
| 4 |
| PH |
| OH |
| 3 |
| 4 |
| 4 |
| 3 |
∵cot∠PAO=
| 2 |
| 3 |
| AH |
| PH |
| 2 |
| 3 |
| 2 |
| 3 |
∵OA=OH+AH=6,∴
| 4 |
| 3 |
| 2 |
| 3 |
∴y=3.∴x=4.
∴点P的坐标为(4,3). (1分)
(2)设所求二次函数的解析式为y=ax2+bx+c.
由题意,得
|
解得
|
∴所求二次函数的解析式为y=-
| 3 |
| 8 |
| 9 |
| 4 |
(3)设点M的坐标为(3,y),二次函数的对称轴与OP相交于点C.
由题意,得 点C的坐标为(3,
| 9 |
| 4 |
∴S△MOP=S△COM+S△PCM=
| 1 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
| 9 |
| 4 |
(1分)
而S△MOP=S△AOP,S△AOP=
| 1 |
| 2 |
∴2(
| 9 |
| 4 |
| 9 |
| 4 |

∴点M的坐标为(3,-
| 9 |
| 4 |
另解:设二次函数的对称轴与x轴交于点B,连接MA.
∵△MOP与△AOP的面积相等,且OP是公共边,
∴点M到OP与点A到OP的距离相等. (1分)
∴AM∥OP.
∴∠MAB=∠POA.(1分)
∴tan∠MAB=tan∠POA=
| 3 |
| 4 |
∵AB=3,∴
| BM |
| 3 |
| 3 |
| 4 |
∴BM=
| 9 |
| 4 |
∴点M的坐标为(3,-
| 9 |
| 4 |
点评:本题考查了二次函数的综合运用.关键是利用直角三角形的边角关系求点P的坐标,根据二次函数的图象经过O、A、P三点,求抛物线解析式,根据三角形面积相等,列方程求M点的坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
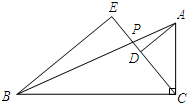 (2007•上海模拟)已知:如图,Rt△ABC中,∠ACB=90°,P是边AB上一点,AD⊥CP,BE⊥CP,垂足分别为D、E,已知AB=
(2007•上海模拟)已知:如图,Rt△ABC中,∠ACB=90°,P是边AB上一点,AD⊥CP,BE⊥CP,垂足分别为D、E,已知AB=