题目内容
如图,在直角坐标系xOy中,二次函数图象的顶点坐标为C(4,-| 3 |
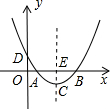 为6.
为6.(1)求二次函数的解析式;
(2)设抛物线与y轴的交点为D,求四边形DACB的面积;
(3)在x轴上方的抛物线上,是否存在点P,使得∠PAC被x轴平分?如果存在,请求出P点的坐标;如果不存在,请说明理由.
分析:(1)已知了抛物线的顶点坐标即可得出抛物线的对称轴方程,结合AB的长度即可求出A、B的坐标,进而可用待定系数法求出抛物线的解析式;
(2)根据抛物线的解析式易求得D点坐标,可将四边形DACB的面积分成△DAB和△ABC两部分来求;
(3)此题可通过构建相似三角形求解,过P作PF⊥x轴于F,设抛物线的对称轴与x轴的交点为E,若∠PAC被x轴平分,那么△APF∽△ACE,根据相似三角形所得到的比例线段即可求出P点的坐标.
(2)根据抛物线的解析式易求得D点坐标,可将四边形DACB的面积分成△DAB和△ABC两部分来求;
(3)此题可通过构建相似三角形求解,过P作PF⊥x轴于F,设抛物线的对称轴与x轴的交点为E,若∠PAC被x轴平分,那么△APF∽△ACE,根据相似三角形所得到的比例线段即可求出P点的坐标.
解答: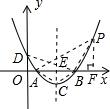 解:
解:
(1)根据题意,得:OE=4,AE=BE=3
∴OA=1,OB=7即A(1,0)、B(7,0)
设y=a(x-1)(x-7)
∵x=4,y=-
,∴a=
所求解析式为y=
(x-1)(x-7)(或y=
x2-
x+
)
(2)连接DA、AC、BC、DB
当x=0时,y=
,∴D(0,
)
∴S四边形DACB=S△DAB+S△ACB=
×6×
+
×6×
=
(3)假设存在点P(x,y),使x轴平分∠PAC,过点P作PF⊥x轴,垂足为点F
则△APF∽△ACE
∴
=
,即:
=
3(
x2-
x+
)=
(x-1)
∴x2-11x+10=0,x1=10,x2=1
当x=10时,y=
×(10-1)×(10-7)=3
当x=1时,y=0(不合题意,舍去)
∴P(10,3
).
 解:
解:(1)根据题意,得:OE=4,AE=BE=3
∴OA=1,OB=7即A(1,0)、B(7,0)
设y=a(x-1)(x-7)
∵x=4,y=-
| 3 |
| ||
| 9 |
所求解析式为y=
| ||
| 9 |
| ||
| 9 |
8
| ||
| 9 |
7
| ||
| 9 |
(2)连接DA、AC、BC、DB
当x=0时,y=
7
| ||
| 9 |
7
| ||
| 9 |
∴S四边形DACB=S△DAB+S△ACB=
| 1 |
| 2 |
7
| ||
| 9 |
| 1 |
| 2 |
| 3 |
| 16 |
| 3 |
| 3 |
(3)假设存在点P(x,y),使x轴平分∠PAC,过点P作PF⊥x轴,垂足为点F
则△APF∽△ACE
∴
| PF |
| CE |
| AF |
| AE |
| y | ||
|
| x-1 |
| 3 |
3(
| ||
| 9 |
8
| ||
| 9 |
7
| ||
| 9 |
| 3 |
∴x2-11x+10=0,x1=10,x2=1
当x=10时,y=
| ||
| 9 |
| 3 |
当x=1时,y=0(不合题意,舍去)
∴P(10,3
| 3 |
点评:此题主要考查了二次函数解析式的确定、图形面积的求法以及相似三角形的判定和性质.

练习册系列答案
相关题目
 是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.
是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.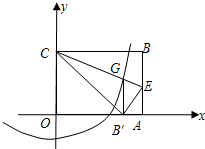 半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标. 已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.
已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D. 如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.
如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.