题目内容
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A( ![]() ,1)在反比例函数y=
,1)在反比例函数y= ![]() 的图象上.
的图象上.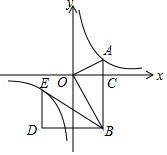
(1)求k的值;
(2)若将△BOA绕点B按逆时针方向旋转60°,得到△BDE,判断点E是否在该反比例函数的图象上,并说明理由.
【答案】
(1)
解:∵点A( ![]() ,1)在反比例函数y=
,1)在反比例函数y= ![]() 的图象上,
的图象上,
∴k= ![]() ×1=
×1= ![]()
(2)
解:点E在该反比例函数的图象上,理由如下:
∵A( ![]() ,1),
,1),
∴OA= ![]() =2,
=2,
由OA⊥OB,AB⊥x轴,易证△AOC∽△ABO,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴AB=4,
∴OB= ![]() =2
=2 ![]() ,
,
∴sin∠ABO= ![]() =
= ![]() =
= ![]() ,
,
∴∠ABO=30°.
∵将△BOA绕点B按逆时针方向旋转60°得到△BDE,
∴△BOA≌△BDE,∠OBD=60°,
∴BO=BD=2 ![]() ,OA=DE=2,∠BOA=∠BDE=90°,
,OA=DE=2,∠BOA=∠BDE=90°,
∠ABD=30°+60°=90°.
又BD﹣OC=2 ![]() ﹣
﹣ ![]() =
= ![]() ,BC﹣DE=4﹣1﹣2=1,
,BC﹣DE=4﹣1﹣2=1,
∴E(﹣ ![]() ,﹣1),
,﹣1),
∵﹣ ![]() ×
× ![]() ,
,
∴点E在该反比例函数的图象上
【解析】(1)将点A( ![]() ,1)代入y=
,1)代入y= ![]() ,利用待定系数法即可求出反比例函数的表达式;(2)先解△OAB,得出∠ABO=30°,再根据旋转的性质求出E点坐标为(﹣
,利用待定系数法即可求出反比例函数的表达式;(2)先解△OAB,得出∠ABO=30°,再根据旋转的性质求出E点坐标为(﹣ ![]() ,﹣1),即可求解.
,﹣1),即可求解.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目