题目内容
20.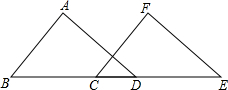 如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠ADB=∠FCE.
如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠ADB=∠FCE.
分析 根据等式的性质得出BD=CE,再利用SAS得出:△ABD与△FEC全等,进而得出∠ADB=∠FCE.
解答 证明:∵BC=DE,
∴BC+CD=DE+CD,
即BD=CE,
在△ABD与△FEC中,
$\left\{\begin{array}{l}{AB=EF}\\{∠B=∠E}\\{BD=EC}\end{array}\right.$,
∴△ABD≌△FEC(SAS),
∴∠ADB=∠FCE.
点评 此题考查全等三角形的判定和性质,关键是根据等式的性质得出BD=CE,再利用全等三角形的判定和性质解答.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
8.化简$\sqrt{12}$的结果是( )
| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{6}$ |
5.计算(-xy3)2的结果是( )
| A. | x2y6 | B. | -x2y6 | C. | x2y9 | D. | -x2y9 |
12.圆内接四边形ABCD中,已知∠A=70°,则∠C=( )
| A. | 20° | B. | 30° | C. | 70° | D. | 110° |
9.将圆心角为90°,面积为4πcm2的扇形围成一个圆锥的侧面,则所围成的圆锥的底面半径为( )
| A. | 1cm | B. | 2cm | C. | 3cm | D. | 4cm |
17.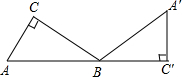 在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )
在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )
 在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )
在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )| A. | $\frac{5}{2}π$ | B. | $\frac{{5\sqrt{3}}}{3}π$ | C. | $\frac{{4\sqrt{3}}}{3}π$ | D. | 2π |