题目内容
 竖直向上发射的小球的高度h(m)关于运动时间t(s)的函数表达式为h=
竖直向上发射的小球的高度h(m)关于运动时间t(s)的函数表达式为h=| 1 |
| 2π |
| A、3s | B、3.5s |
| C、4s | D、6.5s |
考点:二次函数的应用
专题:
分析:根据题中已知条件求出函数h=
t2+πt的对称轴t=4,四个选项中的时间越接近4小球就越高.
| 1 |
| 2π |
解答:解:由题意可知:h(2)=h(6),则函数h=
t2+πt的对称轴t=
=4,
故在t=4s时,小球的高度最高,
故选:C.
| 1 |
| 2π |
| 6+2 |
| 2 |
故在t=4s时,小球的高度最高,
故选:C.
点评:本题主要考查了二次函数的实际应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键,属于中档题.

练习册系列答案
相关题目
若|x|=3,y=7,则x-y的值是( )
| A、±4 | B、±10 |
| C、-4或-10 | D、±4,10 |
下列判断正确的是( )
| A、近似数0.380是精确到0.01 |
| B、近似数5.6万是精确到十分位 |
| C、近似数300是精确到百位 |
| D、近似数1.60×103是精确到十位 |
已知a+b=2,求代数式a2-b2+4b的值为( )
| A、8 | B、4 | C、-4 | D、-8 |
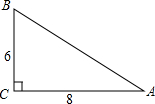 某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长分别为6m、8m.现要将其扩建成等腰三角形,且扩充部分是以8m为直角边长的直角三角形.请你设计出所有合适的方案,画出草图,并求出扩建后的等腰三角形花圃的面积.
某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长分别为6m、8m.现要将其扩建成等腰三角形,且扩充部分是以8m为直角边长的直角三角形.请你设计出所有合适的方案,画出草图,并求出扩建后的等腰三角形花圃的面积.