Question

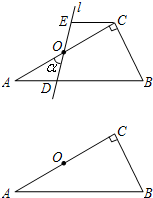如图，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2．点O是AC的中点，过点O的直线l从与AC重合的位置开始，绕点O作逆时针旋转，交AB边于点D，过点C作CE∥AB交直线l于点E，设直线l的旋转角为α．
（1）①当α=

 

度时，四边形EDBC是等腰梯形，此时AD的长为

 

；
②当α=

 

度时，四边形EDBC是直角梯形，此时AD的长为

 

；
（2）当α=90°时，判断四边形EDBC是否为菱形，并说明理由．

Answer 1

分析：（1）根据旋转的性质和等腰梯形的性质，①假设四边形EDBC是等腰梯形，根据题目已知条件及外角和定理可求α，AD；②假设四边形EDBC是直角梯形，根据题目已知条件及内角和定理可求α，AD．
（2）根据∠α=∠ACB=90°先证明四边形EDBC是平行四边形．再利用Rt△ABC中，∠ACB=90°，∠B=60°，BC=2求得AB，AC，AO的长度；在Rt△AOD中，∠A=30°，AD=2，可求BD，比较得BD=BC，可证明四边形EDBC是菱形．

解答：解：（1）①当四边形EDBC是等腰梯形时，
∵∠EDB=∠B=60°，而∠A=30°，
∴α=∠EDB-∠A=30°，
∴△ADO是等腰三角形，
∴AD=OD，
过点O作OF∥BC，
∵BC⊥AC，
∴OF⊥AC，
∴OF是△ABC的中位线，
∴OF=

1

2

BC=1，
∵α=∠EDB-∠A=30°，
∴∠ODF=60°=∠DOF=60°，
∴△ODF是等边三角形，
∴OD=OF=DF=1，
∵∠A=∠α=30°，
∴AD=OD=1；

②当四边形EDBC是直角梯形时，∠ODA=90°，而∠A=30°，
根据三角形的内角和定理，得α=90°-∠A=60°，此时，AD=

1

2

AC×

3

2

=1.5．

（2）当∠α=90°时，四边形EDBC是菱形．
∵∠α=∠ACB=90°，
∴BC∥ED，
∵CE∥AB，
∴四边形EDBC是平行四边形．
在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2，
∴∠A=30°，
∴AB=4，AC=2

3

，
∴AO=

1

2

AC=

3

．
在Rt△AOD中，∠A=30°，OD=

1

2

AD，
AD=

AO2+OD2

=

( 3 )2+( 1 2 AD)2

，
∴AD=2，
∴BD=2，
∴BD=BC．
又∵四边形EDBC是平行四边形，
∴四边形EDBC是菱形．

点评：解决此问题，既要弄清等腰梯形、直角梯形及菱形的判定，又要掌握有关旋转的知识，在直角三角形中，30度角所对的直角边等于斜边的一半，也是解决问题的关键．