Question

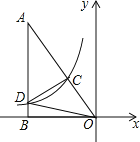
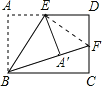
【题目】如图，矩形ABCD中，AB=1，E、F分别为AD、CD的中点，沿BE将△ABE折叠，若点A恰好落在BF上，则AD= ．

Answer 1

【答案】．

【解析】

试题分析：连接EF，则可证明△EA′F≌△EDF，从而根据BF=BA′+A′F，得出BF的长，在Rt△BCF中，利用勾股定理可求出BC，即得AD的长度．

解：连接EF，

∵点E、点F是AD、DC的中点，

∴AE=ED，CF=DF=CD=AB=，

由折叠的性质可得AE=A′E，

∴A′E=DE，

在Rt△EA′F和Rt△EDF中，

∵，

∴Rt△EA′F≌Rt△EDF（HL），

∴A′F=DF=，

∴BF=BA′+A′F=AB+DF=1+=，

在Rt△BCF中，BC==．

∴AD=BC=．

故答案为：．