题目内容
设a、b、c、x、y、z都是整数,且同时满足a2+b2+c2=25,x2+y2+z2=36,ax+by+cz=30,则 =________.
=________.

分析:根据a、b、c、x、y、z都是整数,当满足a2+b2+c2=25时,存在两种可能:①一个为0,另外两个为3,4;②两个为0,另一个为5.当满足x2+y2+z2=36,只有一种可能,一个为6,其它两个为0.再由ax+by+cz=30,可得出①不符合题意,然后代入即可.
解答:根据a、b、c、x、y、z都是整数,
(1)当满足a2+b2+c2=25时,存在两种可能:①一个为0,另外两个为3,4;②两个为0,另一个为5.
(2)当满足x2+y2+z2=36,只有一种可能,一个为6,其它两个为0.
再由ax+by+cz=30,可得出(1)中的①不符合题意,
故
 =
= =
= .
.故答案为:
 .
.点评:本题考查了分式的化简求值,难度较大,主要是掌握分类讨论的思想解题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
八年级某班级部分同学去植树,若每人平均植树7棵,还剩9棵,若每人平均植树9棵,则有1名同学植树的棵数不到8棵.若设同学人数为x人,下列各项能准确的求出同学人数与种植的树木的数量的是( )
| A、7x+9-9(x-1)>0 | |||||
| B、7x+9-9(x-1)<8 | |||||
C、
| |||||
D、
|
 已知⊙O1的半径为R,周长为C.
已知⊙O1的半径为R,周长为C.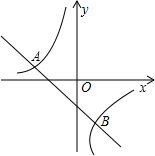 如图,若反比例函数y=-
如图,若反比例函数y=-