题目内容
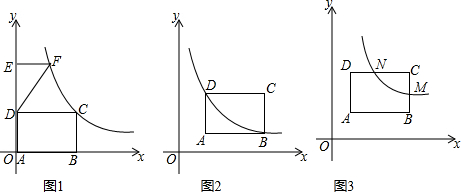
2.如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线0M为抛物线的一部分),则下列结论:①BC=BE=5cm;②$\frac{AB}{BE}$=$\frac{3}{5}$;③当0<t≤5时,y=$\frac{2}{5}$t2;④矩形ABCD的面积是10cm2.
其中正确的结论是①③(填序号).

分析 根据图②可以判断三角形的面积变化分为三段,可以判断出当点P到达点E时点Q到达点C,从而得到BC、BE的长度,再根据M、N是从5秒到7秒,可得ED的长度,然后表示出AE的长度,根据勾股定理求出AB的长度,然后针对各小题分析解答即可.
解答 解:①根据图②可得,当点P到达点E时点Q到达点C,
∵点P、Q的运动的速度都是1cm/s,
∴BC=BE=5cm,故①正确;
②∵从M到N的变化是2秒,
∴DE=2,
∴AE=5-2=3,
∴AB=$\sqrt{{BE}^{2}-{AE}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴$\frac{AB}{BE}$=$\frac{4}{5}$,故②错误;
③如图,过点P作PF⊥BC于点F,
根据面积不变时△BPQ的面积为10,可得AB=4,
∵AD∥BC,
∴∠AEB=∠PBF,
∴sin∠PBF=sin∠AEB=$\frac{AE}{BE}$=$\frac{4}{5}$,
∴PF=PBsin∠PBF=$\frac{4}{5}$t,
∴当0<t≤5时,y=$\frac{1}{2}$BQ•PF=$\frac{1}{2}$t•$\frac{4}{5}$t=$\frac{2}{5}$t2,故③正确;
④∵AB=4cm,BC=5cm,
∴S矩形ABCD=4×5=20cm2,故④错误.
故答案为:①③.
点评 本题考查的是动点问题的函数图象,能根据题意得出矩形的边长是解答此题的关键.

练习册系列答案
相关题目
10.下列说法错误的是( )
| A. | 6是-6的相反数 | B. | -6是-(-6)的相反数 | ||
| C. | -(+8)与+(-8)互为相反数 | D. | +(-8)与-(-8)互为相反数 |
17.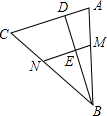 如图所示,在△ABC中,MN∥AC,BD⊥AC于点D,交MN于点E,则下列说法中,不正确的是( )
如图所示,在△ABC中,MN∥AC,BD⊥AC于点D,交MN于点E,则下列说法中,不正确的是( )
 如图所示,在△ABC中,MN∥AC,BD⊥AC于点D,交MN于点E,则下列说法中,不正确的是( )
如图所示,在△ABC中,MN∥AC,BD⊥AC于点D,交MN于点E,则下列说法中,不正确的是( )| A. | BD是△ABC的高 | B. | CD是△BCD的高 | C. | ME是△ABD的高 | D. | BE是△BMN的高 |
7.下列说法正确的是( )
| A. | 正数和负数统称为有理数 | B. | 0是最小的自然数 | ||
| C. | 整数就是自然数 | D. | 负数就是有负号的数 |
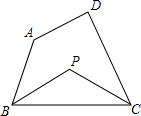 如图,在四边形ABCD中,∠A+∠D=220°,∠ABC的平分线与∠BCD的平分线交于点P,则∠P的度数为110°.
如图,在四边形ABCD中,∠A+∠D=220°,∠ABC的平分线与∠BCD的平分线交于点P,则∠P的度数为110°.