题目内容
如图所示,折线A-B-C是一段登山石阶,其中AB=BC,AB部分的坡角为60°,BC部分的坡角为45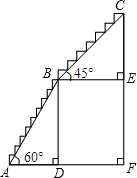 °,AD=30m.
°,AD=30m.
(1)求石阶路(折线A→B→C)的长.
(2)如果每级石阶的高不超过20cm,那么这一段登山石阶至少有多少级台阶?(最后一级石阶的高度不足20cm时,按一级石阶计算.可能用到的数据: ,
, )
)
解:(1)∵∠BAD=60°,AD=30m,
∴∠ABD=30°,AB=2AD=60m,
而AB=BC
∴BC=60m,
∴石阶路(折线A→B→C)的长为120m;
(2)∵BD= AD=30
AD=30 m,
m,
CE= BC=30
BC=30 m,
m,
∴CF=30( +
+ )m
)m
∴30( +
+ )×100÷20≈472,
)×100÷20≈472,
∴这一段登山石阶至少有472级台阶.
分析:(1)由∠BAD=60°,AD=30m,根据含30度的直角三角形三边的关系,得到AB=2AD=60m,则BC=60m,所以石阶路(折线A→B→C)的长为120m;
(2)根据含30度的直角三角形三边的关系和等腰直角三角形的性质得到BD= AD=30
AD=30 m,CE=
m,CE= BC=30
BC=30 m,则30(
m,则30( +
+ )×100÷20≈472.
)×100÷20≈472.
点评:本题考查了坡度的概念:斜坡的坡度等于斜坡的铅直高度与对应的水平距离的比值,即斜坡的坡度等于斜坡的坡角的正弦.也考查了含30度的直角三角形三边的关系和等腰直角三角形的性质.
∴∠ABD=30°,AB=2AD=60m,
而AB=BC
∴BC=60m,
∴石阶路(折线A→B→C)的长为120m;
(2)∵BD=
 AD=30
AD=30 m,
m,CE=
 BC=30
BC=30 m,
m,∴CF=30(
 +
+ )m
)m∴30(
 +
+ )×100÷20≈472,
)×100÷20≈472,∴这一段登山石阶至少有472级台阶.
分析:(1)由∠BAD=60°,AD=30m,根据含30度的直角三角形三边的关系,得到AB=2AD=60m,则BC=60m,所以石阶路(折线A→B→C)的长为120m;
(2)根据含30度的直角三角形三边的关系和等腰直角三角形的性质得到BD=
 AD=30
AD=30 m,CE=
m,CE= BC=30
BC=30 m,则30(
m,则30( +
+ )×100÷20≈472.
)×100÷20≈472.点评:本题考查了坡度的概念:斜坡的坡度等于斜坡的铅直高度与对应的水平距离的比值,即斜坡的坡度等于斜坡的坡角的正弦.也考查了含30度的直角三角形三边的关系和等腰直角三角形的性质.

练习册系列答案
相关题目
 如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.
如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象. (2012•新疆)某校九年级一班班长统计去年1~8月“校园文化”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,这组数据的中位数是
(2012•新疆)某校九年级一班班长统计去年1~8月“校园文化”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,这组数据的中位数是 (2013•桥东区二模)某市农业科学研究所几年前在甲乙两座荒山上,各栽种了100棵苹果树,成活率是98%现已结果成熟,为了分析收成情况,分别从两山上随机各采摘了4棵树上的苹果,每棵果树的产量如图所示的折线统计图
(2013•桥东区二模)某市农业科学研究所几年前在甲乙两座荒山上,各栽种了100棵苹果树,成活率是98%现已结果成熟,为了分析收成情况,分别从两山上随机各采摘了4棵树上的苹果,每棵果树的产量如图所示的折线统计图 (2013•南京二模)甲车以某一速度沿公路从A地匀速驶往B地,到达B地停留m小时后,立即以原速沿原路匀速返回A地,共用11小时.甲车出发一段时间后,乙车沿同一条公路以每小时120千米的速度从A地匀速驶往B地,甲车从A地出发9小时后,两车在距离A地160千米处相遇,甲车回到A地的同时乙车到达了B地.如图所示的折线是甲车离A地的距离y1(千米)与行驶时间 x(小时)之间的函数图象.
(2013•南京二模)甲车以某一速度沿公路从A地匀速驶往B地,到达B地停留m小时后,立即以原速沿原路匀速返回A地,共用11小时.甲车出发一段时间后,乙车沿同一条公路以每小时120千米的速度从A地匀速驶往B地,甲车从A地出发9小时后,两车在距离A地160千米处相遇,甲车回到A地的同时乙车到达了B地.如图所示的折线是甲车离A地的距离y1(千米)与行驶时间 x(小时)之间的函数图象.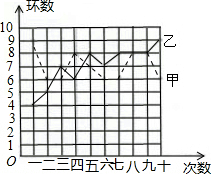 射击集训队在一个月的集训中,对甲、乙两名运动员进行了10次测试,
射击集训队在一个月的集训中,对甲、乙两名运动员进行了10次测试,