题目内容
抛物线y=2x2,y=-2x2,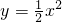 共有的性质是
共有的性质是
- A.开口向下
- B.对称轴是y轴
- C.都有最低点
- D.y随x的增大而减小
B
分析:根据二次函数的性质解题.
解答:(1)y=2x2开口向上,对称轴为y轴,有最低点,顶点为原点;
(2)y=-2x2开口向下,对称轴为y轴,有最高点,顶点为原点;
(3)y= x2开口向上,对称轴为y轴,有最低点,顶点为原点.
x2开口向上,对称轴为y轴,有最低点,顶点为原点.
故选B.
点评:考查二次函数顶点式y=a(x-h)2+k的性质.二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:
①当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<- 时,y随x的增大而减小;x>-
时,y随x的增大而减小;x>- 时,y随x的增大而增大;x=-
时,y随x的增大而增大;x=- 时,y取得最小值
时,y取得最小值 ,即顶点是抛物线的最低点.
,即顶点是抛物线的最低点.
②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<- 时,y随x的增大而增大;x>-
时,y随x的增大而增大;x>- 时,y随x的增大而减小;x=-
时,y随x的增大而减小;x=- 时,y取得最大值
时,y取得最大值 ,即顶点是抛物线的最高点.
,即顶点是抛物线的最高点.
分析:根据二次函数的性质解题.
解答:(1)y=2x2开口向上,对称轴为y轴,有最低点,顶点为原点;
(2)y=-2x2开口向下,对称轴为y轴,有最高点,顶点为原点;
(3)y=
 x2开口向上,对称轴为y轴,有最低点,顶点为原点.
x2开口向上,对称轴为y轴,有最低点,顶点为原点.故选B.
点评:考查二次函数顶点式y=a(x-h)2+k的性质.二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:
①当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
 时,y随x的增大而减小;x>-
时,y随x的增大而减小;x>- 时,y随x的增大而增大;x=-
时,y随x的增大而增大;x=- 时,y取得最小值
时,y取得最小值 ,即顶点是抛物线的最低点.
,即顶点是抛物线的最低点.②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
 时,y随x的增大而增大;x>-
时,y随x的增大而增大;x>- 时,y随x的增大而减小;x=-
时,y随x的增大而减小;x=- 时,y取得最大值
时,y取得最大值 ,即顶点是抛物线的最高点.
,即顶点是抛物线的最高点. 
练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目