题目内容
 如图,格点图中的每个小方格都是边长为1的正方形. 在建立平面直角坐标系后,点A(-2,0),B(2,0).(下列画图要求均为格点图形且不得超出已给格点图).
如图,格点图中的每个小方格都是边长为1的正方形. 在建立平面直角坐标系后,点A(-2,0),B(2,0).(下列画图要求均为格点图形且不得超出已给格点图).(1)画出Rt△ABC,使得tan∠CAB=
| 1 |
| 2 |
(2,2)
(2,2)
;(2)把(1)中Rt△ABC以点A为位似中心放大,使放大前后对应边长的比为2:3,画出△AB'C'的图形;
(3)是否存在点D(已知点除外),使得在Rt△ACD中满足tan∠CAD=
| 1 |
| 2 |
(3,0)
(3,0)
;若不存在,则直接回答不存在.分析:(1)找出能满足△ABC是直角三角形点C,再结合tan∠CAB=
,可得出点C的坐标.
(2)分别连接并延长位似中心和能代表原图的关键点,根据位似比为2:3可得出△AB'C'.
(3)根据题意,找到直角三角形ACD即可.
| 1 |
| 2 |
(2)分别连接并延长位似中心和能代表原图的关键点,根据位似比为2:3可得出△AB'C'.
(3)根据题意,找到直角三角形ACD即可.
解答:解:(1)

点C、C'、C''均能满足△ABC是直角三角形,
又∵tan∠CAB=
,
∴只有点C的位置满足题意,此时点C的坐标为(2,2).
(2)分别连接并延长位似中心和能代表原图的关键点,得到各点的对应点,顺次连接如下:

(3)∵tan∠CAD=
 ,
,
∴△ACD满图题意,
此时点D的坐标为(3,0).

点C、C'、C''均能满足△ABC是直角三角形,
又∵tan∠CAB=
| 1 |
| 2 |
∴只有点C的位置满足题意,此时点C的坐标为(2,2).
(2)分别连接并延长位似中心和能代表原图的关键点,得到各点的对应点,顺次连接如下:

(3)∵tan∠CAD=
| 1 |
| 2 |
 ,
,∴△ACD满图题意,
此时点D的坐标为(3,0).
点评:此题考查了解直角三角形的应用、位似作图的知识,解答本题的关键是熟练掌握直角三角形中各角三角函数的表示形式,难度一般.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 15、如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心的坐标是
15、如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心的坐标是
 如图,格点图中的每个小方格都是边长为1的正方形. 在建立平面直角坐标系后,点A(-2,0),B(2,0).(下列画图要求均为格点图形且不得超出已给格点图).
如图,格点图中的每个小方格都是边长为1的正方形. 在建立平面直角坐标系后,点A(-2,0),B(2,0).(下列画图要求均为格点图形且不得超出已给格点图). ,并写出C点坐标______;
,并写出C点坐标______;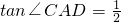 ,若存在,请写出D点坐标______;若不存在,则直接回答不存在.
,若存在,请写出D点坐标______;若不存在,则直接回答不存在. ,并写出C点坐标______;
,并写出C点坐标______; ,若存在,请写出D点坐标______;若不存在,则直接回答不存在.
,若存在,请写出D点坐标______;若不存在,则直接回答不存在.