题目内容
在1，2，3，…，100中，不能被2整除也不能被5整除的所有整数的乘积的个位数字是（ ）
分析：先写出不能被2及5整除的数相乘的形式，然后根据乘数的形式可将各因式合并，继而可得出答案．
解答：解：根据题意得：所求为：1×3×7×9×11×13×17×19…×91×93×97×99的个位数字，
等于310×710×910的个位数字，
等于2110×815的个位数字，
故个位数字为1．
故选B．
等于310×710×910的个位数字，
等于2110×815的个位数字，
故个位数字为1．
故选B．
点评：本题主要考查数的整除性问题，难度较大，技巧性也较强，关键是得出不能被2整除也不能被5整除的所有整数的乘积的个位数字等于2110×815的个位数字．
练习册系列答案
相关题目
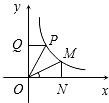设P（a，b），M（c，d）是反比例函数y=
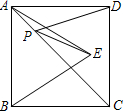如图所示，正方形ABCD的面积为18，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（ ）
20、如图，在△ABC中，点D，E分别是AB，AC边的中点，若把△ADE绕着点E顺时针旋转180°得到△CFE．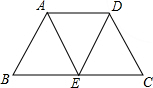
在等腰梯形ABCD中，AD∥BC，E是BC的中点，连接AE，DE，AE与DE相等吗？
