题目内容
萧山区教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动。教育局就“学生体育活动兴趣爱好”的问题,随机调查了本区的部分初中生,并根据调查结果绘制成以下图表:
 |
(1)请将以上图中空缺部分补充完整;
(2)请计算出教育局共随机调查了本区多少名初中生?并计算出这些学生中参加跳长绳人数所在扇形的圆心角的度数;
(3)若全区共有12000名初中生,请你估算出参加踢毽子的学生人数。
(1)补全图形如下:
|

问题提出
平面内不在同一条直线上的三点确定一个圆.那么平面内的四点(任意三点均不在同一
直线上),能否在同一个圆呢?
初步思考
设不在同一条直线上的三点A、B、C确定的圆为⊙O.
⑴当C、D在线段AB的同侧时,
如图①,若点D在⊙O上,此时有∠ACB=∠ADB,理由是 ;
如图②,若点D在⊙O内,此时有∠ACB ∠ADB;
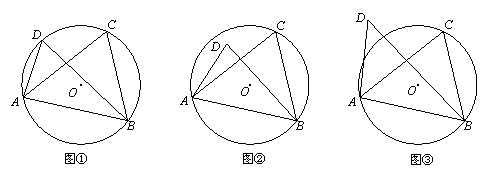 如图③,若点D在⊙O外,此时有∠ACB ∠ADB.(填“=”、“>”或“<”);
如图③,若点D在⊙O外,此时有∠ACB ∠ADB.(填“=”、“>”或“<”);
由上面的探究,请直接写出A、B、C、D四点在同一个圆上的条件: .
类比学习
(2)仿照上面的探究思路,请探究:当C、D在线段AB的异侧时的情形.
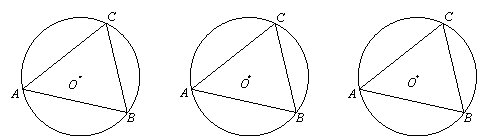 |
此时有 , 此时有 , 此时有 .
由上面的探究,请用文字语言直接写出A、B、C、D四点在同一个圆上的条件: .
拓展延伸
 (3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
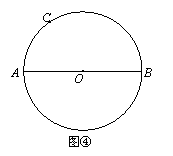
已知:如图,AB是⊙O的直径,点C在⊙O上.
求作:CN⊥AB.
作法:①连接CA,CB;
②在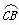 上任取异于B、C的一点D,连接DA,DB;
上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB于M;
⑤连接D、M并延长,交⊙O于N.连接CN.
则CN⊥AB.
请按上述作法在图④中作图,并说明CN⊥AB的理由.(提示:可以利用(2)中的结论)
在篮球比赛中,某队员连续10场比赛中每场的得分情况如下表所示:
| 场次(场) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 得分(分) | 13 | 4 | 13 | 16 | 6 | 19 | 4 | 4 | 7 | 38 |
则这10场比赛中他得分的中位数和众数分别是( )
A.10,4 B.10,7 C.7,13 D.13,4
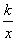 ,当k>0时,y随x的增大而减少;
,当k>0时,y随x的增大而减少; ,规定
,规定 ,若
,若 ,则
,则 的值为 。
的值为 。 A.
A.  B. 2 C.
B. 2 C.  D.
D. 
