题目内容
(1) +
+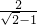 -4
-4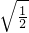 -2(
-2( )0
)0
(2)(10 -6
-6 +4
+4 )÷
)÷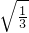
(3) •(-
•(- )÷3
)÷3
(4)(7+4 )(2-
)(2- )2.
)2.
解:(1)原式=3 +2(
+2( +1)-2
+1)-2 -2
-2
=3 +2
+2 +2-2
+2-2 -2
-2
=3 ;
;
(2)原式=(40 -18
-18 +8
+8 )×
)×
=30 ×
×
=90;
(3)原式=2b •(-
•(- a
a )•
)•

=-a2 ;
;
(4)原式=(7+4 )(7-4
)(7-4 )
)
=49-48
=1.
分析:(1)根据零指数幂和分母有理化得到原式=3 +2(
+2( +1)-2
+1)-2 -2,然后去括号合并即可;
-2,然后去括号合并即可;
(2)先把括号内各二次根式化为最简二次根式和除法运算化为乘法运算,然后合并后进行二次根式的乘法运算;
(3)先把各二次根式化为最简二次根式,然后进行二次根式的乘除运算;
(4)先利用完全平方公式计算,然后利用平方差公式计算.
点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂.
 +2(
+2( +1)-2
+1)-2 -2
-2=3
 +2
+2 +2-2
+2-2 -2
-2=3
 ;
;(2)原式=(40
 -18
-18 +8
+8 )×
)×
=30
 ×
×
=90;
(3)原式=2b
 •(-
•(- a
a )•
)•

=-a2
 ;
;(4)原式=(7+4
 )(7-4
)(7-4 )
)=49-48
=1.
分析:(1)根据零指数幂和分母有理化得到原式=3
 +2(
+2( +1)-2
+1)-2 -2,然后去括号合并即可;
-2,然后去括号合并即可;(2)先把括号内各二次根式化为最简二次根式和除法运算化为乘法运算,然后合并后进行二次根式的乘法运算;
(3)先把各二次根式化为最简二次根式,然后进行二次根式的乘除运算;
(4)先利用完全平方公式计算,然后利用平方差公式计算.
点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂.

练习册系列答案
相关题目
天羽服装厂生产M、N型两种服装,受资金及规模限制,每天最多只能用A种面料68米 和B种面料62米生产M、N型两种服装共80套.已知M、N型服装每套所需面料和成本如下表,设每天生产M型服装x套.
和B种面料62米生产M、N型两种服装共80套.已知M、N型服装每套所需面料和成本如下表,设每天生产M型服装x套.
| A | B | 成本 | |
| M型 | 1.1m | 0.4m | 100元 |
| N型 | 0.6m | 0.9m | 80元 |
(2)经市场调查,生产的M、N型服装有两种销售方案(假设每天生产的服装都能全部售出).
方案Ⅰ:两种型号服装都在本市销售,M型180元/件、N型120元/件;
方案Ⅱ:N型服装在本市销售,120元/件,M型服装批发给H市服装商,其每件的批发价y(元)与批量x(件)之间的关系如图所示.
如果你是厂长,应采用哪种销售方案可使每天获利最大,最大利润是多少?并确定相应的生产方案.

 如图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动.如果点Q从点A出发,沿图中所示方向按A?B?C?D?A滑动到A止,同时点R从点B出发,沿图中所示方向按B?C?D?A?B滑动到B止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积为
如图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动.如果点Q从点A出发,沿图中所示方向按A?B?C?D?A滑动到A止,同时点R从点B出发,沿图中所示方向按B?C?D?A?B滑动到B止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积为 还多10人.请你算一算,参加清洁工作的团员和非团员各为多少人?
还多10人.请你算一算,参加清洁工作的团员和非团员各为多少人? 如图,△ABC中,∠C=90°,⊙O分别切AB、BC、AC于D、E、F,若AD=3cm,BD=2cm,试求⊙O的半径.
如图,△ABC中,∠C=90°,⊙O分别切AB、BC、AC于D、E、F,若AD=3cm,BD=2cm,试求⊙O的半径. 已知:如图,AC⊥OD,AE⊥OF,BD⊥OD,BF⊥OF,AC=AE,求证:BD=BF.
已知:如图,AC⊥OD,AE⊥OF,BD⊥OD,BF⊥OF,AC=AE,求证:BD=BF.