题目内容
 如图,将边长都为1cm的正方形按如图所示摆放,点A1、A2、A3、A4分别是正方形的中心,则前5个这样的正方形重叠部分的面积和为( )
如图,将边长都为1cm的正方形按如图所示摆放,点A1、A2、A3、A4分别是正方形的中心,则前5个这样的正方形重叠部分的面积和为( )分析:过点A1分别作正方形两边的垂线A1D与A1E,根据正方形的性质可得A1D=A1E,四边形A1EA2D是正方形,再根据同角的余角相等求出∠BA1D=∠CA1E,然后利用“角边角”证明△A1BD和△A1CE全等,根据全等三角形的面积相等求出阴影部分的面积等于正方形面积的
,同理可求所有阴影部分的面积都是正方形的面积的
,然后根据正方形的面积列式计算即可.
| 1 |
| 4 |
| 1 |
| 4 |
解答: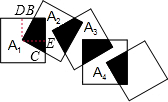 解:如图,过点A1分别作正方形两边的垂线A1D与A1E,
解:如图,过点A1分别作正方形两边的垂线A1D与A1E,
∵点A1是正方形的中心,
∴A1D=A1E,四边形A1EA2D是正方形,
∴∠BA1D+∠BA1E=90°,
又∵∠CA1E+∠BA1E=90°,
∴∠BA1D=∠CA1E,
在△A1BD和△A1CE中,
,
∴△A1BD≌△A1CE(ASA),
∴△A1BD的面积=△A1CE的面积,
∴阴影部分的面积=正方形A1EA2D的面积=
×12=
,
同理可求,每一个阴影部分的面积都是正方形面积的
,为
,
∴重叠部分的面积和=
×4=1.
故选C.
 解:如图,过点A1分别作正方形两边的垂线A1D与A1E,
解:如图,过点A1分别作正方形两边的垂线A1D与A1E,∵点A1是正方形的中心,
∴A1D=A1E,四边形A1EA2D是正方形,
∴∠BA1D+∠BA1E=90°,
又∵∠CA1E+∠BA1E=90°,
∴∠BA1D=∠CA1E,
在△A1BD和△A1CE中,
|
∴△A1BD≌△A1CE(ASA),
∴△A1BD的面积=△A1CE的面积,
∴阴影部分的面积=正方形A1EA2D的面积=
| 1 |
| 4 |
| 1 |
| 4 |
同理可求,每一个阴影部分的面积都是正方形面积的
| 1 |
| 4 |
| 1 |
| 4 |
∴重叠部分的面积和=
| 1 |
| 4 |
故选C.
点评:本题考查了正方形的性质,全等三角形的判定与性质,作辅助线构造出全等三角形求出阴影部分的面积是正方形的面积的
是解题的关键.
| 1 |
| 4 |

练习册系列答案
相关题目
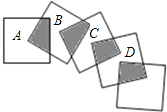 如图,所示,将五个边长都为1cm的正方形按如图所示摆放,其中点A、B、C、D分别是正方形对角线的交点、如果有n个这样大小的正方形这样摆放,则阴影面积的总和是
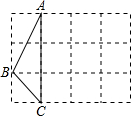
如图,所示,将五个边长都为1cm的正方形按如图所示摆放,其中点A、B、C、D分别是正方形对角线的交点、如果有n个这样大小的正方形这样摆放,则阴影面积的总和是 如图,在边长均为1cm的正方形网格中,△ABC的三个顶点和点A′均在格点上.将△ABC向右平移,使点A平移至点A′处,得到△A′B′C′.在图中画出△A′B′C′,并求边AC扫过的图形面积.
如图,在边长均为1cm的正方形网格中,△ABC的三个顶点和点A′均在格点上.将△ABC向右平移,使点A平移至点A′处,得到△A′B′C′.在图中画出△A′B′C′,并求边AC扫过的图形面积. 如图,将边长都为1cm的正方形按如图所示摆放,点A1、A2、A3、A4分别是正方形的中心,则前5个这样的正方形重叠部分的面积和为
如图,将边长都为1cm的正方形按如图所示摆放,点A1、A2、A3、A4分别是正方形的中心,则前5个这样的正方形重叠部分的面积和为

 如图,在边长均为1cm的正方形网格中,△ABC的三个顶点均在格点上.将△ABC绕点A逆时针旋转90°,得到△AB′C′.
如图,在边长均为1cm的正方形网格中,△ABC的三个顶点均在格点上.将△ABC绕点A逆时针旋转90°,得到△AB′C′.